Tính Diện Tích Tam Giác Cân
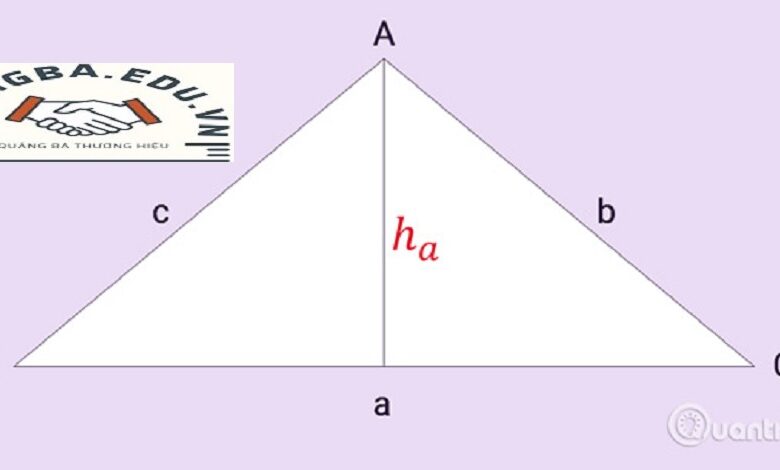
Tính Diện Tích Tam Giác Cân – Tam giác cân là một loại tam giác đặc biệt trong hình học, được định nghĩa bởi hai cạnh và hai góc bằng nhau. Điều này có nghĩa là trong tam giác cân, hai cạnh bên có độ dài bằng nhau và hai góc đối diện với hai cạnh đó cũng bằng nhau. Tính chất này làm cho tam giác cân trở thành một đối tượng nghiên cứu quan trọng và thường xuất hiện trong các bài toán hình học cơ bản.
Giới thiệu về tam giác cân
Một đặc điểm nổi bật của tam giác cân là trục đối xứng của nó. Trục đối xứng này đi qua đỉnh của góc không bằng hai góc còn lại và điểm giữa của cạnh đối diện. Trục đối xứng này chia tam giác cân thành hai tam giác vuông cân bằng nhau. Điều này không chỉ giúp trong việc phân tích hình học mà còn rất hữu ích trong các bài toán liên quan đến tính diện tích và chu vi của tam giác cân.
Tam giác cân có một số tính chất hình học đáng chú ý. Đầu tiên, trong tam giác cân, đường cao từ đỉnh của góc không bằng hai góc còn lại sẽ đồng thời là trung tuyến và phân giác của góc đó. Thứ hai, tổng ba góc trong tam giác cân luôn bằng 180 độ, giống như mọi tam giác khác. Tuy nhiên, với hai góc bằng nhau, chúng ta có thể dễ dàng xác định góc còn lại khi biết giá trị của một trong hai góc bằng nhau.
Bài viết liên quan: Phần mềm Monkey Junior
Những đặc điểm này khiến tam giác cân trở thành một trong những hình dạng cơ bản và quan trọng trong hình học. Sự hiểu biết về tam giác cân không chỉ giúp trong việc giải các bài toán hình học mà còn cung cấp nền tảng cho việc nghiên cứu các hình dạng phức tạp hơn. Trong phần tiếp theo, chúng ta sẽ đi sâu hơn vào việc tính toán diện tích của tam giác cân, một ứng dụng thực tế và phổ biến của kiến thức về tam giác cân.
Công thức tính diện tích tam giác cân
Để tính diện tích tam giác cân, công thức cơ bản nhất thường được sử dụng là: A = 1/2 * b * h. Trong đó, ‘A’ là diện tích, ‘b’ là độ dài của đáy, và ‘h’ là chiều cao của tam giác cân. Công thức này rất phổ biến và dễ hiểu, giúp chúng ta nhanh chóng xác định diện tích khi đã biết độ dài của đáy và chiều cao.
Trường hợp bạn không biết chiều cao của tam giác cân, nhưng biết độ dài của hai cạnh bên và góc ở đỉnh, bạn vẫn có thể tính được diện tích. Để làm điều này, trước tiên cần xác định chiều cao của tam giác. Chiều cao có thể được tính bằng cách sử dụng hàm số cosine trong tam giác vuông. Giả sử cạnh bên là ‘a’ và góc ở đỉnh là ‘θ’, chiều cao ‘h’ có thể được tính bằng công thức: h = a * sin(θ).
Sau khi tính được chiều cao, bạn có thể áp dụng lại công thức cơ bản A = 1/2 * b * h để tìm diện tích. Ví dụ, nếu cạnh bên của tam giác cân là 5 cm và góc ở đỉnh là 30 độ, bạn có thể tính chiều cao như sau: h = 5 * sin(30) = 5 * 0.5 = 2.5 cm. Tiếp theo, áp dụng công thức diện tích với ‘b’ là độ dài đáy và ‘h’ là chiều cao vừa tính được.
Công thức này rất hữu ích trong nhiều tình huống khác nhau, đặc biệt khi các thông tin về tam giác không đầy đủ. Bằng cách sử dụng các phương pháp toán học cơ bản, bạn có thể dễ dàng tính toán diện tích tam giác cân với độ chính xác cao.
Ví dụ minh họa
Để hiểu rõ hơn về cách tính diện tích tam giác cân, chúng ta sẽ cùng xem xét một số ví dụ cụ thể. Những ví dụ này không chỉ giúp minh họa cách áp dụng công thức mà còn cung cấp các bài toán thực tế với các bước giải chi tiết.
Ví dụ 1: Giả sử chúng ta có một tam giác cân với đáy là 6 cm và chiều cao tương ứng từ đỉnh đến đáy là 4 cm. Để tính diện tích tam giác cân này, ta sử dụng công thức:
Diện tích = (1/2) * đáy * chiều cao
Áp dụng công thức, ta có:
Diện tích = (1/2) * 6 cm * 4 cm = 12 cm²
Ví dụ 2: Xét một tam giác cân khác với cạnh đáy là 10 cm và chiều cao là 5 cm. Áp dụng công thức tính diện tích, chúng ta có:
Diện tích = (1/2) * 10 cm * 5 cm = 25 cm²
Ví dụ 3: Một bài toán thực tế hơn, giả sử bạn muốn tính diện tích của một tam giác cân trong một khu vườn. Tam giác này có cạnh đáy dài 8 m và chiều cao từ đỉnh đến đáy là 6 m. Sử dụng công thức tính diện tích, ta có:
Diện tích = (1/2) * 8 m * 6 m = 24 m²
Những ví dụ trên giúp chúng ta thấy rõ cách áp dụng công thức tính diện tích tam giác cân trong các trường hợp cụ thể. Việc xác định đúng các yếu tố như đáy và chiều cao là rất quan trọng để đảm bảo kết quả tính toán chính xác.
Ứng dụng của tam giác cân trong thực tế
Tam giác cân, một khái niệm toán học cơ bản, không chỉ xuất hiện trong toán học mà còn có nhiều ứng dụng thực tế trong đời sống hàng ngày và các lĩnh vực khác nhau. Trong kiến trúc, tam giác cân thường được sử dụng để tạo nên các cấu trúc bền vững và thẩm mỹ. Ví dụ, các mái nhà thường có hình dạng tam giác cân để giúp phân phối lực đều, giảm nguy cơ sụp đổ và tăng tính ổn định. Các cấu trúc này không chỉ bền mà còn có vẻ đẹp hài hòa, tạo cảm giác cân đối cho người nhìn.
Trong kỹ thuật, tam giác cân cũng đóng vai trò quan trọng. Các kỹ sư thường sử dụng hình dạng này để thiết kế các bộ phận máy móc và cấu trúc xây dựng. Đặc biệt trong thiết kế cầu, các cấu trúc tam giác cân được sử dụng để tạo các hệ thống giàn chịu lực, giúp cầu có thể chịu được trọng tải lớn và các tác động từ môi trường xung quanh. Tính đối xứng và khả năng phân phối lực của tam giác cân làm cho nó trở thành lựa chọn lý tưởng trong các ứng dụng kỹ thuật.
Ngoài ra, trong nghệ thuật, tam giác cân cũng xuất hiện dưới dạng các hình vẽ và tác phẩm điêu khắc. Nghệ sĩ thường sử dụng tam giác cân để tạo ra các tác phẩm có tính thẩm mỹ cao, nhấn mạnh vào sự cân đối và hài hòa. Tam giác cân không chỉ mang lại vẻ đẹp mà còn giúp tác phẩm trở nên thu hút và dễ nhìn.
Như vậy, tam giác cân không chỉ có ứng dụng trong toán học mà còn có vai trò quan trọng trong nhiều lĩnh vực khác. Từ kiến trúc, kỹ thuật đến nghệ thuật, tam giác cân góp phần tạo nên những công trình bền vững, đẹp mắt và ổn định.
Các bài toán nâng cao về tam giác cân
Trong lĩnh vực hình học, tam giác cân là một đối tượng nghiên cứu phong phú với nhiều tính chất độc đáo. Để hiểu sâu hơn về diện tích tam giác cân, chúng ta sẽ khám phá các bài toán nâng cao, bao gồm cả những bài toán có điều kiện phức tạp hơn và yêu cầu sự hiểu biết toàn diện về các nguyên lý hình học. Đặc biệt, chúng ta sẽ xem xét các bài toán về tam giác cân nội tiếp và ngoại tiếp các đường tròn, cũng như các tính chất đặc biệt khác của tam giác cân.
Một trong những bài toán phổ biến liên quan đến tam giác cân là việc tính diện tích khi tam giác cân nội tiếp một đường tròn. Để giải quyết bài toán này, ta cần sử dụng bán kính đường tròn và độ dài các cạnh của tam giác. Định lý Cosine và công thức tính diện tích tam giác dựa trên bán kính và độ dài cạnh là những công cụ hữu ích trong trường hợp này.
Ngoài ra, các bài toán về tam giác cân ngoại tiếp một đường tròn cũng mang đến những thử thách đặc biệt. Để giải quyết, chúng ta cần áp dụng các định lý về đường tròn và tam giác như định lý về đường tròn ngoại tiếp, cùng với các kiến thức về tỉ lệ và đối xứng của tam giác cân. Việc xác định chính xác vị trí của các điểm tiếp xúc giữa tam giác và đường tròn ngoại tiếp là một bước quan trọng để tính toán diện tích một cách chính xác.
Không chỉ dừng lại ở các bài toán về nội tiếp và ngoại tiếp, tam giác cân còn được nghiên cứu thông qua các tính chất đặc biệt như độ dài các đường trung tuyến, đường cao, và đường phân giác. Những tính chất này không chỉ giúp trong việc tính diện tích mà còn cung cấp cái nhìn sâu sắc về cấu trúc hình học của tam giác cân. Việc hiểu rõ và áp dụng các tính chất này sẽ giúp giải quyết các bài toán phức tạp một cách hiệu quả và chính xác.
Lỗi thường gặp khi tính toán
Khi tính diện tích tam giác cân, có nhiều lỗi phổ biến mà người học và thực hành thường gặp phải. Một trong những lỗi thông thường nhất là nhầm lẫn giữa các cạnh và góc của tam giác. Trong tam giác cân, hai cạnh bên bằng nhau và góc đối diện cạnh đáy cũng bằng nhau. Nhầm lẫn giữa các cạnh và góc này có thể dẫn đến việc sử dụng sai công thức, từ đó tính toán sai diện tích.
Một lỗi khác là sử dụng sai công thức tính diện tích. Công thức cơ bản để tính diện tích tam giác là (đáy x chiều cao) / 2. Tuy nhiên, đối với tam giác cân, việc xác định đúng chiều cao từ đỉnh xuống cạnh đáy là cực kỳ quan trọng. Nhiều người thường tính sai chiều cao, hoặc sử dụng các công thức khác nhau mà không hiểu rõ đặc điểm của tam giác cân.
Không kiểm tra lại kết quả tính toán cũng là một lỗi khá phổ biến. Sau khi tính toán xong, việc kiểm tra lại các bước và kết quả là cần thiết để đảm bảo tính chính xác. Nhiều người bỏ qua bước này và dẫn đến các sai sót không đáng có trong kết quả cuối cùng.
Để tránh những lỗi này, người học cần nắm vững các đặc điểm cơ bản của tam giác cân, bao gồm các cạnh và góc. Sử dụng đúng công thức và kiểm tra kỹ lưỡng từng bước trong quá trình tính toán cũng là những biện pháp quan trọng. Việc làm quen với các lỗi phổ biến và biết cách khắc phục sẽ giúp tăng độ chính xác trong các bài toán liên quan đến tam giác cân.
Tài liệu tham khảo và nguồn học thêm
Việc hiểu rõ và áp dụng chính xác cách tính diện tích tam giác cân đòi hỏi người học cần có sự tiếp cận từ nhiều nguồn tài liệu đa dạng. Dưới đây là một số tài liệu tham khảo và nguồn học thêm hữu ích để giúp bạn đọc mở rộng kiến thức về tam giác cân và các khái niệm liên quan.
Đầu tiên, các sách giáo khoa về toán học từ cấp trung học cơ sở đến trung học phổ thông như “Hình Học 7” và “Hình Học 9” của Nhà xuất bản Giáo dục Việt Nam là những nguồn tài liệu cơ bản và cần thiết. Những cuốn sách này không chỉ cung cấp lý thuyết mà còn đưa ra nhiều bài tập minh họa, giúp học sinh nắm vững cách tính diện tích tam giác cân thông qua thực hành.
Đối với những ai muốn tìm hiểu sâu hơn, các bài báo khoa học như “Properties of Isosceles Triangles and Their Applications” đăng trên tạp chí Mathematics Journal có thể là một nguồn tài liệu quý giá. Những bài báo này thường cung cấp các phân tích chi tiết và các ứng dụng thực tiễn của tam giác cân trong nhiều lĩnh vực khác nhau.
Bên cạnh đó, các trang web học tập như Khan Academy, Coursera và các kênh YouTube giáo dục như Mathologer và 3Blue1Brown cũng cung cấp nhiều video giảng dạy trực quan và sinh động về tam giác cân. Những tài liệu số này không chỉ tiện lợi mà còn giúp người học tiếp cận kiến thức một cách dễ dàng và thú vị hơn.
Cuối cùng, các diễn đàn học tập trực tuyến như Stack Exchange và Reddit cũng là nơi bạn có thể trao đổi, đặt câu hỏi và tìm kiếm sự trợ giúp từ cộng đồng người học và giáo viên trên toàn thế giới. Việc tham gia vào những cộng đồng này sẽ giúp bạn làm rõ những thắc mắc và học hỏi từ kinh nghiệm của người khác.
Kết luận
Trong bài viết này, chúng ta đã thảo luận chi tiết về cách tính diện tích tam giác cân, một khái niệm quan trọng trong toán học. Việc hiểu và áp dụng đúng công thức tính diện tích tam giác cân không chỉ giúp bạn giải quyết các bài toán một cách chính xác mà còn củng cố nền tảng kiến thức toán học của bạn.
Bài viết xem thêm: Sơ Đồ Tư Duy Đất Nước
Công thức tính diện tích tam giác cân có thể được áp dụng trong nhiều tình huống thực tế, từ các bài toán học đường đến các ứng dụng trong kỹ thuật và khoa học. Việc nắm vững kiến thức này sẽ giúp bạn tự tin hơn khi đối mặt với các vấn đề liên quan đến hình học.