Q là Tập Hợp Số Gì?
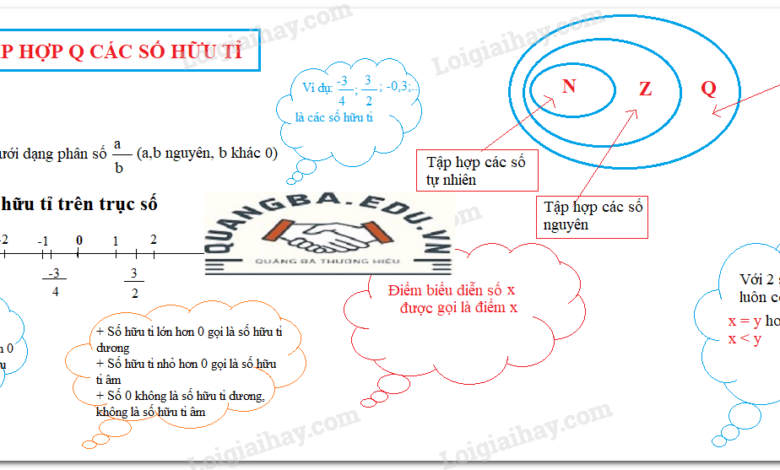
Q là Tập Hợp Số Gì? – Trong toán học, tập hợp số Q đại diện cho tập hợp các số hữu tỉ, một trong những khái niệm cơ bản và quan trọng. Số hữu tỉ là các số có thể biểu diễn dưới dạng phân số, với tử số và mẫu số là các số nguyên và mẫu số khác không. Điều này có nghĩa là bất kỳ số nào có thể được viết dưới dạng a/b, với a và b là các số nguyên và b ≠ 0, đều thuộc tập hợp số Q.
Giới Thiệu về Tập Hợp Số Q
Tập hợp số Q không chỉ đơn giản là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế. Trong toán học, số hữu tỉ được sử dụng để giải quyết các vấn đề về tỷ lệ và tỷ lệ phần trăm, trong khi trong khoa học và kỹ thuật, chúng được áp dụng trong việc đo lường và tính toán chính xác. Ngoài ra, tập hợp số Q còn đóng vai trò quan trọng trong việc phát triển các khái niệm toán học phức tạp hơn, như số thực và số phức.
Q là viết tắt của từ “Quotient” trong tiếng Anh, có nghĩa là thương số, phản ánh bản chất của các số hữu tỉ dưới dạng phân số. Vì vậy, tập hợp số Q bao gồm các số nguyên, các số phân số đơn giản, và cả các số thập phân hữu hạn hoặc vô hạn tuần hoàn. Chẳng hạn, các số như 1/2, -3/4, và 0.75 đều thuộc tập hợp số Q.
Bài viết liên quan: Bán Kính Hình Tròn
Hiểu rõ về tập hợp số Q và các đặc tính của nó giúp chúng ta có cái nhìn sâu sắc hơn về cấu trúc toán học và khả năng ứng dụng của các số hữu tỉ trong nhiều lĩnh vực khác nhau. Từ việc giải các phương trình đơn giản đến phân tích dữ liệu khoa học, số hữu tỉ là một phần không thể thiếu trong kho tàng kiến thức toán học.
Định Nghĩa Tập Hợp Số Q
Tập hợp số Q, hay còn gọi là số hữu tỉ, là một khái niệm quan trọng trong toán học. Định nghĩa cơ bản của tập hợp số Q là tập hợp các số có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b khác 0. Điều này có nghĩa là bất kỳ số nào có thể viết được dưới dạng phân số với tử số và mẫu số là các số nguyên đều thuộc tập hợp số Q. Ví dụ điển hình bao gồm các số như 1/2, -3/4, và cả số nguyên như 5, bởi vì 5 có thể viết lại thành phân số 5/1.
Điểm đặc trưng của số hữu tỉ là chúng bao gồm cả số nguyên và các số thập phân hữu hạn hoặc vô hạn tuần hoàn. Chẳng hạn, số thập phân 0.75 có thể biểu diễn dưới dạng phân số 3/4, do đó nó cũng thuộc tập hợp số Q. Ngược lại, các số thực không thể biểu diễn dưới dạng phân số, như căn bậc hai của 2 hay số pi (π), không thuộc tập hợp số Q.
Việc hiểu và xác định tập hợp số Q giúp phân biệt số hữu tỉ với các loại số khác như số nguyên (tập hợp Z) và số thực (tập hợp R). Trong khi số nguyên chỉ bao gồm các số không có phần thập phân, và số thực bao gồm tất cả các số có thể tồn tại trên trục số, số hữu tỉ tập trung vào những số có thể được biểu diễn dưới dạng phân số. Điều này làm cho tập hợp số Q trở thành một phần quan trọng trong các lý thuyết và ứng dụng toán học.
Lịch Sử và Phát Triển của Tập Hợp Số Q
Tập hợp số Q, hay còn gọi là tập hợp các số hữu tỉ, đã trở thành một phần không thể thiếu của toán học từ rất lâu đời. Sự khám phá và nghiên cứu về các số hữu tỉ có thể được truy nguyên về thời kỳ cổ đại, khi các nhà toán học Hy Lạp như Pythagoras bắt đầu nghiên cứu về các số này. Pythagoras và các học trò của ông đã phát hiện ra rằng các số có thể được biểu diễn dưới dạng thương của hai số nguyên, một khái niệm cơ bản của số hữu tỉ.
Qua nhiều thế kỷ, khái niệm về số hữu tỉ đã được các nhà toán học tiếp tục phát triển và hoàn thiện. Vào thế kỷ thứ 3 trước Công nguyên, nhà toán học Eudoxus đã đưa ra lý thuyết về tỷ lệ, một bước ngoặt quan trọng trong sự hiểu biết về các số hữu tỉ. Lý thuyết này đã giúp các nhà toán học có thể so sánh và tính toán với các số hữu tỉ một cách chính xác hơn.
Đến thời kỳ Trung cổ, các nhà toán học Ả Rập như Al-Khwarizmi đã tiếp tục nghiên cứu và phát triển các phương pháp tính toán với số hữu tỉ. Họ đã khám phá ra nhiều tính chất và ứng dụng mới của các số này, mở rộng phạm vi và sự hiểu biết về tập hợp số Q.
Vào thời kỳ Phục Hưng, các nhà toán học châu Âu như Leonardo Fibonacci đã áp dụng các khái niệm về số hữu tỉ vào nhiều bài toán thực tế, từ đó đẩy mạnh sự phát triển của toán học. Fibonacci, với công trình nổi tiếng “Liber Abaci,” đã giới thiệu hệ thống số Ả Rập và các phương pháp tính toán mới, bao gồm việc sử dụng số hữu tỉ trong thương mại và tài chính.
Trong thời gian gần đây, các nhà toán học hiện đại tiếp tục khám phá và ứng dụng số hữu tỉ trong nhiều lĩnh vực khác nhau, từ lý thuyết số học đến phân tích toán học. Tập hợp số Q không chỉ là một phần quan trọng của toán học lý thuyết mà còn có nhiều ứng dụng thực tiễn trong khoa học và kỹ thuật.

Tính Chất Của Số Hữu Tỉ
Số hữu tỉ, còn gọi là số phân số, là tập hợp các số có thể biểu diễn dưới dạng a/b, trong đó a và b là các số nguyên và b khác 0. Một trong những tính chất đặc biệt của số hữu tỉ là khả năng biểu diễn dưới dạng phân số, điều này giúp chúng dễ dàng xử lý trong các phép tính toán học.
Một tính chất quan trọng khác của số hữu tỉ là phần thập phân của chúng có thể là tuần hoàn hoặc kết thúc. Điều này có nghĩa là khi biểu diễn số hữu tỉ dưới dạng số thập phân, chuỗi số sau dấu phẩy có thể lặp lại theo một mẫu nhất định (tuần hoàn) hoặc dừng lại sau một số chữ số nhất định (kết thúc). Chẳng hạn, số 1/3 có phần thập phân là 0.333… (tuần hoàn), trong khi số 1/2 có phần thập phân là 0.5 (kết thúc).
Những tính chất này của số hữu tỉ rất hữu ích trong các phép tính và ứng dụng toán học. Chúng giúp việc cộng, trừ, nhân, và chia các số này trở nên dễ dàng hơn. Hơn nữa, số hữu tỉ còn được sử dụng rộng rãi trong các lĩnh vực như tài chính, kỹ thuật, và khoa học, nơi mà phép tính chính xác là vô cùng quan trọng.
Với khả năng biểu diễn dưới dạng phân số và phần thập phân tuần hoàn hoặc kết thúc, số hữu tỉ không chỉ giúp đơn giản hóa các phép toán mà còn giúp người học dễ dàng hiểu và áp dụng vào thực tế. Đây là lý do tại sao số hữu tỉ được xem là một trong những nền tảng cơ bản của toán học.
Phân Biệt Số Hữu Tỉ và Số Vô Tỉ
Số học là một lĩnh vực quan trọng trong toán học, và một khía cạnh cơ bản của nó là sự phân biệt giữa số hữu tỉ và số vô tỉ. Hai loại số này khác nhau cơ bản về cách chúng được biểu diễn và các tính chất liên quan.
Số hữu tỉ là những số có thể biểu diễn dưới dạng phân số, tức là dưới dạng a/b với a và b là các số nguyên và b khác 0. Ví dụ, các số như 1/2, -3/4, và 5 đều là số hữu tỉ vì chúng có thể biểu diễn dưới dạng phân số. Số hữu tỉ có phần thập phân hoặc là hữu hạn, hoặc là vô hạn nhưng tuần hoàn. Điều này có nghĩa là sau một số chữ số nhất định, phần thập phân bắt đầu lặp lại một chuỗi các chữ số.
Ngược lại, số vô tỉ là những số không thể biểu diễn dưới dạng phân số. Chúng có phần thập phân vô hạn và không tuần hoàn. Ví dụ nổi bật của số vô tỉ là √2 và π. Số √2, kết quả của căn bậc hai của 2, có phần thập phân kéo dài mãi mãi mà không có chuỗi các chữ số nào lặp lại. Tương tự, số π, đại diện cho tỷ số giữa chu vi và đường kính của một hình tròn, cũng có phần thập phân vô hạn không tuần hoàn.
Phân biệt giữa số hữu tỉ và số vô tỉ là cần thiết để hiểu rõ hơn về cấu trúc của các tập hợp số. Tập hợp số hữu tỉ và tập hợp số vô tỉ cùng nhau tạo nên tập hợp số thực, cung cấp nền tảng cho các khái niệm toán học phức tạp hơn. Việc nắm vững sự khác biệt này không chỉ giúp trong học tập mà còn trong nhiều ứng dụng thực tế liên quan đến số học và toán học.
Ứng Dụng của Số Hữu Tỉ Trong Thực Tiễn
Số hữu tỉ, hay còn gọi là số phân số, có nhiều ứng dụng quan trọng trong thực tiễn. Đầu tiên, trong cuộc sống hàng ngày, chúng ta thường sử dụng số hữu tỉ để thực hiện các phép tính đơn giản như chia sẻ tài nguyên, tính toán chi phí, và đo lường. Ví dụ, khi chia một chiếc bánh thành các phần bằng nhau hoặc khi chia sẻ chi phí giữa các thành viên trong gia đình, số hữu tỉ giúp đảm bảo tính công bằng và chính xác.
Trong lĩnh vực tài chính, số hữu tỉ đóng vai trò quan trọng trong việc tính toán lãi suất, tỷ giá hối đoái, và các khoản đầu tư. Các nhà kinh tế và nhà đầu tư thường sử dụng số hữu tỉ để phân tích và dự đoán xu hướng thị trường, từ đó đưa ra các quyết định tài chính thông minh. Việc trình bày dữ liệu tài chính dưới dạng số hữu tỉ giúp dễ dàng so sánh và hiểu rõ hơn về tình hình tài chính.
Không chỉ dừng lại ở đó, số hữu tỉ còn có ứng dụng rộng rãi trong khoa học và kỹ thuật. Trong lĩnh vực kỹ thuật, việc giải các bài toán thực tế như tính toán lực, diện tích, và thể tích thường yêu cầu sử dụng số hữu tỉ để đạt được độ chính xác cao. Ví dụ, khi thiết kế một công trình xây dựng, các kỹ sư cần sử dụng số hữu tỉ để đảm bảo các kích thước và tỷ lệ phù hợp.
Trong vật lý, số hữu tỉ được sử dụng để biểu diễn các đại lượng như tốc độ, gia tốc, và mật độ. Số liệu chính xác giúp các nhà khoa học tiến hành các thí nghiệm và nghiên cứu một cách hiệu quả hơn. Điều này góp phần quan trọng vào sự phát triển của khoa học và công nghệ.
Tóm lại, số hữu tỉ không chỉ là một khái niệm toán học mà còn là một công cụ hữu ích trong nhiều lĩnh vực của cuộc sống. Từ các phép tính hàng ngày đến các ứng dụng chuyên sâu trong khoa học và kỹ thuật, số hữu tỉ đóng vai trò quan trọng trong việc giúp chúng ta hiểu và giải quyết các vấn đề thực tiễn.
Số Hữu Tỉ Trong Giáo Dục Toán Học
Trong giáo dục, số hữu tỉ là một trong những chủ đề quan trọng được giảng dạy ở các cấp học khác nhau. Từ tiểu học đến đại học, học sinh và sinh viên đều phải nắm vững khái niệm này để có thể tiếp cận các kiến thức toán học cao hơn. Số hữu tỉ, được biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b khác 0, là cơ sở cho nhiều khái niệm toán học khác.
Ở cấp tiểu học, học sinh bắt đầu làm quen với các số hữu tỉ qua việc học các phân số đơn giản. Họ học cách biểu diễn, so sánh và thực hiện các phép tính cơ bản như cộng, trừ, nhân và chia với các phân số. Điều này giúp họ hiểu rõ hơn về mối quan hệ giữa các con số và chuẩn bị cho việc học các khái niệm phức tạp hơn sau này.
Khi lên cấp trung học cơ sở và phổ thông, học sinh tiếp tục mở rộng kiến thức về số hữu tỉ. Họ học cách biến đổi và giải các phương trình có chứa số hữu tỉ, cùng với việc áp dụng các số hữu tỉ trong các bài toán thực tế. Việc nắm vững số hữu tỉ ở cấp độ này là vô cùng quan trọng, vì nó là nền tảng cho nhiều lĩnh vực toán học cao cấp như đại số và hình học.
Tại bậc đại học, sinh viên tiếp tục gặp số hữu tỉ trong nhiều môn học khác nhau, bao gồm cả toán học ứng dụng và lý thuyết. Việc hiểu rõ về số hữu tỉ giúp sinh viên có thể tiếp cận các khái niệm toán học phức tạp hơn như giải tích và lý thuyết số. Nhiều bài toán trong các lĩnh vực này yêu cầu sinh viên phải có kiến thức vững chắc về số hữu tỉ để có thể giải quyết một cách hiệu quả.
Như vậy, số hữu tỉ đóng vai trò then chốt trong giáo dục toán học. Việc nắm vững khái niệm này không chỉ giúp học sinh và sinh viên tiến bộ trong học tập mà còn mở ra cơ hội cho họ trong nhiều lĩnh vực khoa học và kỹ thuật khác nhau.
Kết Luận nội dung Tập Hợp Số Q
Tập hợp số Q, hay còn gọi là tập hợp số hữu tỉ, không chỉ là một khái niệm cơ bản trong toán học, mà còn có vai trò quan trọng trong nhiều lĩnh vực khác nhau. Hiểu rõ về số hữu tỉ giúp chúng ta có khả năng áp dụng chúng một cách hiệu quả trong học tập, nghiên cứu và cuộc sống hàng ngày.
Bài viết xem thêm: Sự Vật Là Gì?
Trong toán học, số hữu tỉ là nền tảng của nhiều khái niệm phức tạp hơn như số thực, số phức và các hàm số. Việc nắm vững tập hợp số Q giúp học sinh và sinh viên xây dựng một kiến thức vững chắc, tạo điều kiện thuận lợi cho việc tiếp thu các kiến thức toán học cao cấp hơn. Điều này không chỉ giới hạn trong toán học mà còn mở rộng ra các ngành khoa học tự nhiên, kỹ thuật và kinh tế.