Đạo hàm là gì?

Đạo hàm là gì? – Trong toán học, đạo hàm là một khái niệm cơ bản đóng vai trò quan trọng trong giải tích. Đạo hàm của một hàm số biểu diễn tốc độ thay đổi của hàm số đó tại một điểm cụ thể khi biến số thay đổi. Nói một cách khác, đạo hàm cung cấp thông tin về độ dốc của đồ thị hàm số ở mỗi điểm, giúp chúng ta hiểu rõ hơn về hành vi của hàm số đó.
Giới thiệu về đạo hàm
Đạo hàm được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kinh tế, kỹ thuật và nhiều ngành khoa học khác. Trong vật lý, đạo hàm biểu diễn tốc độ thay đổi của vị trí theo thời gian, tức là vận tốc. Trong kinh tế, đạo hàm giúp xác định mức độ thay đổi của các biến số kinh tế như lợi nhuận, chi phí, và doanh thu khi các yếu tố đầu vào thay đổi. Trong kỹ thuật, đạo hàm giúp tính toán các tham số quan trọng như tốc độ và gia tốc của các thiết bị và hệ thống.
Bài viết liên quan: Tính Diện Tích Tam Giác Cân
Để tính đạo hàm của một hàm số, ta sử dụng các quy tắc và công thức toán học. Một trong những phương pháp cơ bản để tính đạo hàm là sử dụng định nghĩa của đạo hàm. Định nghĩa này dựa trên giới hạn của tỷ số giữa sự thay đổi của hàm số và sự thay đổi của biến số khi biến số tiến gần đến một giá trị cụ thể. Ngoài ra, còn có nhiều quy tắc và công thức khác như quy tắc chuỗi, quy tắc tích, và quy tắc thương, giúp việc tính toán đạo hàm trở nên dễ dàng và nhanh chóng hơn.
Hiểu rõ về đạo hàm và cách tính toán đạo hàm không chỉ giúp chúng ta giải quyết các bài toán trong toán học mà còn ứng dụng vào nhiều lĩnh vực khác, từ việc mô hình hóa các hiện tượng tự nhiên đến tối ưu hóa các quá trình sản xuất và kinh doanh.
Lịch sử và nguồn gốc của khái niệm đạo hàm
Khái niệm đạo hàm là một trong những phát minh quan trọng nhất trong toán học, được hình thành từ những nghiên cứu sâu rộng vào thế kỷ 17. Những bước đầu tiên trong việc phát triển đạo hàm được ghi nhận qua công trình của hai nhà toán học nổi tiếng: Isaac Newton và Gottfried Wilhelm Leibniz. Mặc dù hoạt động độc lập, cả hai đều đóng vai trò then chốt trong việc xây dựng cơ sở cho giải tích vi phân và tích phân.
Isaac Newton, nhà khoa học người Anh, đã phát triển khái niệm đạo hàm trong quá trình nghiên cứu về chuyển động và lực. Vào những năm 1660, Newton đã giới thiệu một phương pháp mới để giải quyết các vấn đề liên quan đến tốc độ thay đổi của các đại lượng, mà sau này được gọi là “fluxions”. Phương pháp của Newton chủ yếu tập trung vào các ứng dụng vật lý, đặc biệt là trong việc mô tả quỹ đạo của các hành tinh và các vật thể chuyển động.
Ngược lại, Gottfried Wilhelm Leibniz, nhà toán học người Đức, đã phát triển một hệ thống ký hiệu và lý thuyết toán học riêng biệt liên quan đến đạo hàm và tích phân. Vào cuối những năm 1670, Leibniz giới thiệu ký hiệu “dy/dx” để biểu thị đạo hàm, một ký hiệu vẫn còn được sử dụng rộng rãi cho đến ngày nay. Công trình của Leibniz không chỉ giúp đơn giản hóa các tính toán phức tạp mà còn mở ra nhiều hướng nghiên cứu mới trong toán học.
Sự phát triển của giải tích vi phân và tích phân, với đạo hàm là một thành phần cốt lõi, đã tạo ra một cuộc cách mạng trong toán học và khoa học tự nhiên. Những đóng góp của Newton và Leibniz đã đặt nền móng cho nhiều lĩnh vực nghiên cứu hiện đại, từ cơ học lượng tử đến lý thuyết hỗn loạn, và tiếp tục ảnh hưởng sâu rộng đến cách chúng ta hiểu về thế giới tự nhiên.
Định nghĩa và ký hiệu đạo hàm
Đạo hàm của một hàm số \( f(x) \) tại điểm \( x = a \) được định nghĩa là giới hạn của tỉ số giữa sự thay đổi của hàm số và sự thay đổi của biến số khi biến số tiến dần đến \( a \). Cụ thể, đạo hàm tại điểm \( x = a \) được biểu diễn bằng công thức:
\[f'(a) = \lim_{{h \to 0}} \frac{{f(a+h) – f(a)}}{h}\]
Trong công thức trên, \( h \) đại diện cho một sự thay đổi rất nhỏ của biến số \( x \), và giới hạn này biểu thị sự thay đổi nhỏ nhất của hàm số \( f(x) \) khi \( x \) thay đổi từ \( a \) đến \( a+h \). Nếu giới hạn này tồn tại, tức là hàm số \( f(x) \) có đạo hàm tại điểm \( x = a \).
Đạo hàm thường được ký hiệu bằng các ký hiệu khác nhau, tùy thuộc vào ngữ cảnh và ứng dụng cụ thể. Những ký hiệu phổ biến bao gồm:
- f'(x): Đây là ký hiệu phổ biến nhất, biểu thị đạo hàm của hàm số \( f(x) \) tại điểm \( x \).
- \(\frac{df}{dx}\): Ký hiệu này thường được sử dụng trong giải tích và các ứng dụng khoa học kỹ thuật, biểu thị đạo hàm của hàm số \( f(x) \) đối với biến số \( x \).
- Df(x): Ký hiệu này thường xuất hiện trong các ứng dụng toán học cao cấp, biểu thị đạo hàm của hàm số \( f(x) \).
Để hiểu rõ hơn về đạo hàm, hãy xem xét một ví dụ cụ thể. Giả sử ta có hàm số \( f(x) = x^2 \). Đạo hàm của hàm số này là:
\[f'(x) = \lim_{{h \to 0}} \frac{{(x+h)^2 – x^2}}{h} = \lim_{{h \to 0}} \frac{{x^2 + 2xh + h^2 – x^2}}{h} = \lim_{{h \to 0}} \frac{{2xh + h^2}}{h} = \lim_{{h \to 0}} (2x + h) = 2x\]
Như vậy, đạo hàm của hàm số \( f(x) = x^2 \) là \( f'(x) = 2x \). Điều này có nghĩa là độ dốc của hàm số tại mỗi điểm \( x \) là \( 2x \).
Định nghĩa và ký hiệu đạo hàm có ý nghĩa quan trọng trong toán học và các lĩnh vực khoa học ứng dụng, giúp chúng ta hiểu rõ hơn về cách một hàm số thay đổi theo biến số của nó.
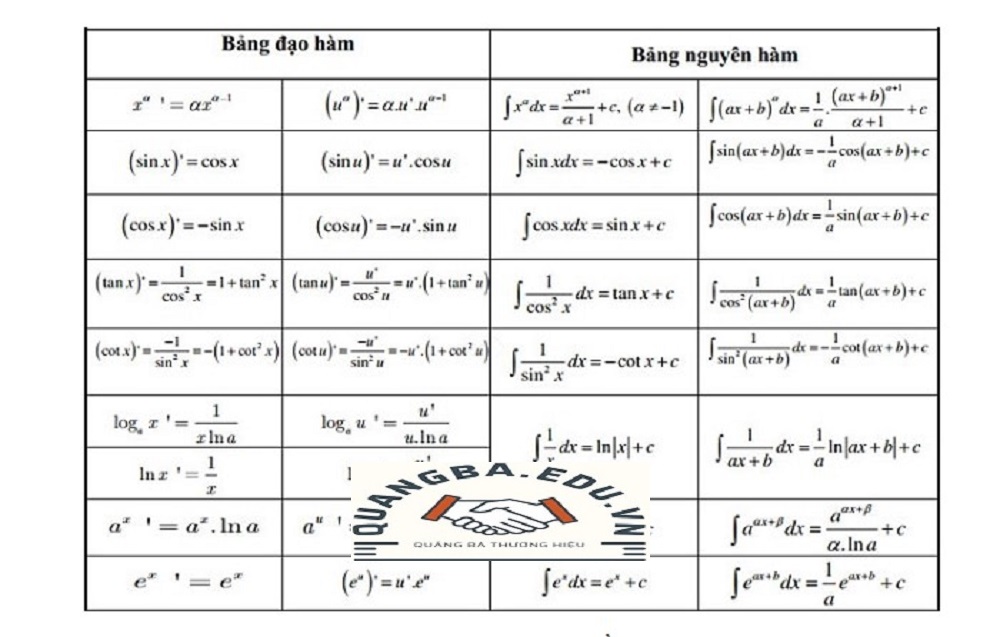
Các quy tắc cơ bản của đạo hàm
Trong việc tính toán đạo hàm, có một số quy tắc cơ bản giúp chúng ta thực hiện các phép tính một cách dễ dàng và chính xác hơn. Những quy tắc này bao gồm quy tắc cộng, quy tắc nhân, quy tắc chia và quy tắc chuỗi. Mỗi quy tắc đều có những ứng dụng cụ thể và mang lại hiệu quả cao trong việc xử lý các hàm số phức tạp.
Quy tắc cộng (Sum Rule) cho phép chúng ta tính đạo hàm của tổng hai hàm số. Nếu \( f(x) \) và \( g(x) \) là hai hàm số có đạo hàm, thì đạo hàm của tổng \( f(x) + g(x) \) bằng tổng của đạo hàm của chúng: \( (f(x) + g(x))’ = f'(x) + g'(x) \). Ví dụ, nếu \( f(x) = 3x^2 \) và \( g(x) = x^3 \), thì đạo hàm của \( f(x) + g(x) \) là \( 6x + 3x^2 \).
Quy tắc nhân (Product Rule) được sử dụng khi cần tính đạo hàm của tích hai hàm số. Nếu \( f(x) \) và \( g(x) \) có đạo hàm, thì đạo hàm của tích \( f(x)g(x) \) được tính bằng công thức: \( (f(x)g(x))’ = f'(x)g(x) + f(x)g'(x) \). Chẳng hạn, nếu \( f(x) = x^2 \) và \( g(x) = e^x \), thì đạo hàm của \( f(x)g(x) \) là \( 2xe^x + x^2e^x \).
Quy tắc chia (Quotient Rule) áp dụng cho việc tính đạo hàm của thương hai hàm số. Nếu \( f(x) \) và \( g(x) \) đều có đạo hàm và \( g(x) \neq 0 \), thì đạo hàm của \( \frac{f(x)}{g(x)} \) được tính bằng: \( \left( \frac{f(x)}{g(x)} \right)’ = \frac{f'(x)g(x) – f(x)g'(x)}{g(x)^2} \). Ví dụ, với \( f(x) = x^2 \) và \( g(x) = x+1 \), đạo hàm của \( \frac{f(x)}{g(x)} \) là \( \frac{2x(x+1) – x^2}{(x+1)^2} \).
Cuối cùng, quy tắc chuỗi (Chain Rule) giúp chúng ta tính đạo hàm của hàm hợp. Nếu \( y = f(u) \) và \( u = g(x) \), thì đạo hàm của \( y = f(g(x)) \) được tính bằng: \( \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \). Ví dụ, nếu \( y = (3x+2)^4 \), thì theo quy tắc chuỗi, đạo hàm của \( y \) là \( 4(3x+2)^3 \cdot 3 = 12(3x+2)^3 \).
Như vậy, việc nắm vững các quy tắc cơ bản của đạo hàm sẽ giúp chúng ta dễ dàng hơn trong việc tính toán đạo hàm của các hàm số phức tạp, giúp tối ưu hóa quá trình học tập và nghiên cứu.
Ứng dụng của đạo hàm trong đời sống
Đạo hàm, một khái niệm lý thuyết cơ bản trong toán học, không chỉ tồn tại trên giấy tờ mà còn có nhiều ứng dụng thực tiễn quan trọng trong đời sống hàng ngày. Một trong những ứng dụng phổ biến nhất của đạo hàm nằm trong lĩnh vực vật lý, cụ thể là tính toán tốc độ và gia tốc. Đạo hàm của vị trí theo thời gian cho ta tốc độ, trong khi đạo hàm của tốc độ theo thời gian cho ta gia tốc. Nhờ đó, chúng ta có thể mô tả chính xác chuyển động của các vật thể, từ việc dự đoán quỹ đạo của hành tinh đến việc thiết kế các phương tiện giao thông an toàn và hiệu quả.
Trong lĩnh vực kinh tế, đạo hàm được sử dụng để tối ưu hóa các chức năng lợi nhuận và chi phí. Bằng cách tính đạo hàm của hàm lợi nhuận hoặc chi phí, chúng ta có thể xác định điểm cực đại hoặc cực tiểu, giúp doanh nghiệp đưa ra các quyết định chiến lược nhằm tối đa hóa lợi nhuận hoặc tối thiểu hóa chi phí. Điều này đặc biệt quan trọng trong việc định giá sản phẩm, quản lý rủi ro và dự báo tài chính.
Không chỉ giới hạn trong vật lý và kinh tế, đạo hàm còn có vai trò quan trọng trong khoa học máy tính, đặc biệt là trong phân tích dữ liệu. Đạo hàm giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các biến số trong một tập dữ liệu lớn, từ đó cải thiện các mô hình dự đoán và thuật toán học máy. Ví dụ, trong học sâu (deep learning), đạo hàm được sử dụng trong quá trình tối ưu hóa hàm mất mát, giúp nâng cao hiệu suất của mô hình.
Những ứng dụng đa dạng của đạo hàm trong đời sống không chỉ làm nổi bật tầm quan trọng của nó trong lý thuyết mà còn chứng minh rằng kiến thức toán học là một công cụ mạnh mẽ để giải quyết các vấn đề thực tiễn.
Phân biệt giữa đạo hàm và vi phân
Đạo hàm và vi phân là hai khái niệm cơ bản trong toán học, đặc biệt trong giải tích. Mặc dù chúng liên quan chặt chẽ với nhau, việc hiểu rõ sự khác biệt giữa chúng là điều cần thiết cho việc áp dụng chúng trong các bài toán khác nhau.
Đạo hàm của một hàm số tại một điểm cụ thể đo lường tốc độ thay đổi của hàm số đó khi biến số thay đổi. Nó được biểu thị bằng ký hiệu f'(x) hoặc dy/dx. Đạo hàm cung cấp thông tin về độ dốc của đường cong tại một điểm cụ thể, giúp chúng ta hiểu rõ hơn về hành vi của hàm số tại điểm đó. Ví dụ, đạo hàm của hàm số y = x^2 tại điểm x = 2 là 4, cho thấy tốc độ thay đổi của y khi x thay đổi tại điểm này là 4.
Vi phân, mặt khác, là sự thay đổi nhỏ của hàm số khi biến số thay đổi một lượng rất nhỏ. Nó được biểu thị bằng ký hiệu dy và liên quan chặt chẽ đến đạo hàm. Vi phân có thể được hiểu như là một cách để ước lượng sự thay đổi của hàm số trong một khoảng thay đổi nhỏ của biến số. Nếu chúng ta biết đạo hàm của hàm số tại một điểm, chúng ta có thể sử dụng đạo hàm đó để tính vi phân. Ví dụ, nếu đạo hàm của hàm số y = x^2 tại điểm x = 2 là 4, vi phân dy khi dx = 0.1 sẽ là dy = 4 * 0.1 = 0.4.
Bài viết xem thêm: Phần mềm Monkey Junior
Như vậy, trong khi đạo hàm cung cấp một giá trị cụ thể tại một điểm, vi phân cung cấp một cách để ước lượng sự thay đổi của hàm số khi biến số thay đổi. Hiểu rõ sự khác biệt giữa hai khái niệm này giúp chúng ta áp dụng chúng hiệu quả trong các bài toán cần tính toán tốc độ thay đổi và sự biến thiên của các hàm số.




