Hiệu là phép tính gì?
Hiệu là phép tính gì? – Phép tính hiệu, hay còn được gọi là phép trừ, là một trong bốn phép tính cơ bản trong toán học. Phép tính này được sử dụng để tìm sự khác biệt giữa hai số. Với vai trò thiết yếu, phép tính hiệu không chỉ được ứng dụng trong các bài toán cơ bản mà còn có tầm quan trọng lớn trong nhiều lĩnh vực khác nhau.
Giới thiệu về phép tính hiệu
Trong cuộc sống hàng ngày, phép tính hiệu giúp chúng ta giải quyết các vấn đề liên quan đến tài chính, quản lý thời gian, và nhiều khía cạnh khác. Ví dụ, khi đi mua sắm, việc tính toán số tiền còn lại sau khi đã mua hàng cần đến phép tính hiệu. Tương tự, trong việc quản lý thời gian, phép tính này giúp xác định khoảng thời gian còn lại sau khi đã hoàn thành một công việc cụ thể.
Không chỉ giới hạn ở cuộc sống hàng ngày, phép tính hiệu còn đóng vai trò quan trọng trong các lĩnh vực khoa học, kinh tế, và kỹ thuật. Trong khoa học, phép tính này được sử dụng để tính toán sai số, xác định mức độ thay đổi của các biến số, và nhiều ứng dụng khác. Trong lĩnh vực kinh tế, phép tính hiệu giúp phân tích các biến động của thị trường, so sánh doanh thu và chi phí để xác định lợi nhuận, và thực hiện các dự báo tài chính.
Bài viết liên quan: Bài Tập Thì Hiện Tại Đơn
Trong kỹ thuật, phép tính hiệu được sử dụng để phân tích và tối ưu hóa các hệ thống, từ việc tính toán mức tiêu thụ năng lượng, xác định lượng nguyên liệu cần thiết, đến việc đánh giá hiệu quả của các giải pháp kỹ thuật khác nhau. Nhờ có phép tính hiệu, các kỹ sư và nhà khoa học có thể đưa ra các quyết định chính xác và hiệu quả hơn trong quá trình nghiên cứu và ứng dụng thực tiễn.
Định nghĩa và ký hiệu của phép tính hiệu
Phép tính hiệu, hay còn gọi là phép trừ, là một trong bốn phép tính cơ bản của toán học. Định nghĩa của phép tính hiệu là quá trình lấy một số, được gọi là số bị trừ, trừ đi một số khác, được gọi là số trừ. Kết quả thu được từ phép tính này được gọi là hiệu, hay còn gọi là kết quả của phép trừ.
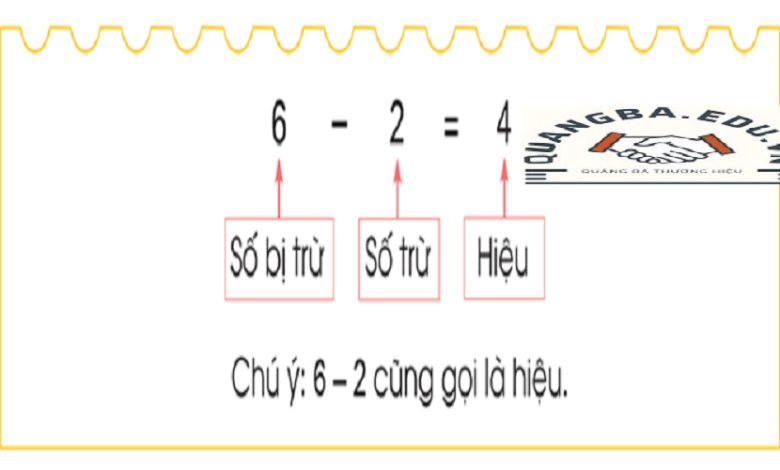
Ký hiệu của phép tính hiệu là dấu trừ (-). Ví dụ, trong biểu thức 8 – 3 = 5, số 8 là số bị trừ, số 3 là số trừ, và số 5 là kết quả của phép tính hiệu. Biểu thức này có thể được đọc là “tám trừ ba bằng năm”. Phép tính hiệu là một phần quan trọng trong toán học cơ bản và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau của cuộc sống hàng ngày.
Phép tính hiệu không chỉ giúp chúng ta xác định sự khác biệt giữa hai số mà còn được sử dụng để giải quyết nhiều vấn đề phức tạp hơn trong toán học và các lĩnh vực khoa học khác. Ví dụ, trong kinh tế học, phép tính hiệu có thể được sử dụng để tính toán lợi nhuận sau khi trừ đi chi phí. Trong vật lý, nó có thể được sử dụng để tính toán sự thay đổi trong các đại lượng như vận tốc hoặc năng lượng.
Hiểu rõ về định nghĩa và ký hiệu của phép tính hiệu là một bước quan trọng để tiếp cận các khái niệm toán học phức tạp hơn. Việc nắm vững phép tính cơ bản này sẽ giúp chúng ta dễ dàng hơn trong việc học tập và ứng dụng toán học vào thực tiễn. Với sự hiểu biết vững chắc về phép tính hiệu, chúng ta có thể tự tin giải quyết các bài toán từ đơn giản đến phức tạp, từ học thuật đến thực tế.
Tính chất của phép tính hiệu
Phép tính hiệu, trong toán học, có những tính chất đặc trưng mà người học cần nắm vững. Một trong những tính chất quan trọng nhất của phép tính hiệu là tính không giao hoán. Điều này có nghĩa rằng khi thực hiện phép tính hiệu giữa hai số, thứ tự của các số là rất quan trọng. Cụ thể, a – b không bằng b – a. Ví dụ, nếu a = 5 và b = 3, thì 5 – 3 bằng 2, trong khi 3 – 5 bằng -2. Tính chất này làm nổi bật sự khác biệt so với phép cộng và nhân, những phép toán có tính giao hoán.
Không chỉ dừng lại ở đó, phép tính hiệu còn không có tính kết hợp. Điều này có nghĩa là khi thực hiện phép tính hiệu với nhiều hơn hai số, việc thay đổi thứ tự thực hiện phép toán sẽ dẫn đến kết quả khác nhau. Cụ thể, (a – b) – c không bằng a – (b – c). Ví dụ, nếu a = 10, b = 5, và c = 2, thì (10 – 5) – 2 bằng 3, trong khi 10 – (5 – 2) bằng 7. Tính chất này yêu cầu người thực hiện phép toán phải tuân theo thứ tự nhất định để đạt được kết quả chính xác.
Những tính chất này của phép tính hiệu làm cho nó trở nên đặc biệt và đòi hỏi sự chú ý cẩn thận khi thực hiện các phép toán liên quan. Hiểu rõ và áp dụng đúng các tính chất này sẽ giúp người học tránh được những sai lầm không đáng có và làm việc với các phép toán một cách hiệu quả hơn.
Ứng dụng của phép tính hiệu trong cuộc sống
Phép tính hiệu, hay phép trừ, đóng vai trò quan trọng trong cuộc sống hàng ngày của chúng ta. Từ các hoạt động đơn giản như tính toán chi tiêu đến các công việc phức tạp hơn như đo lường khoảng cách hay quản lý thời gian, phép tính hiệu luôn hiện diện.
Ví dụ, trong việc tính toán chi tiêu hàng ngày, khi bạn có một số tiền ban đầu và bạn chi tiêu một phần trong số đó, phép tính hiệu sẽ giúp bạn biết được số tiền còn lại. Giả sử bạn có 100.000 đồng và bạn mua một món hàng giá 30.000 đồng, số tiền còn lại sẽ là 100.000 đồng trừ đi 30.000 đồng, tức là 70.000 đồng.
Trong lĩnh vực đo lường, phép tính hiệu cũng rất hữu ích. Khi bạn cần xác định khoảng cách giữa hai điểm, bạn có thể sử dụng phép trừ để tìm ra sự khác biệt. Chẳng hạn, nếu bạn biết khoảng cách từ nhà bạn đến trường là 10 km và từ nhà bạn đến trạm xe buýt là 3 km, bạn có thể tính được khoảng cách từ trạm xe buýt đến trường là 10 km trừ đi 3 km, tương đương 7 km.
Quản lý thời gian cũng là một lĩnh vực mà phép tính hiệu được ứng dụng rộng rãi. Khi bạn cần xác định thời gian cần thiết để hoàn thành một công việc, phép trừ giúp bạn biết được khoảng thời gian còn lại. Ví dụ, nếu bạn có một cuộc họp lúc 15:00 và hiện tại là 14:30, phép trừ sẽ giúp bạn biết rằng bạn còn 30 phút để chuẩn bị.
Như vậy, phép tính hiệu không chỉ là một khái niệm toán học cơ bản mà còn là một công cụ hữu ích trong nhiều khía cạnh của cuộc sống hàng ngày, từ quản lý tài chính cá nhân đến quản lý thời gian và đo lường khoảng cách.
Ứng dụng của phép tính hiệu trong khoa học và kỹ thuật
Trong lĩnh vực khoa học và kỹ thuật, phép tính hiệu đóng vai trò quan trọng trong việc đo lường sự thay đổi và xác định sự khác biệt giữa các giá trị. Phép tính này không chỉ đơn thuần là một công cụ toán học mà còn là cơ sở cho nhiều ứng dụng thực tiễn trong vật lý, kỹ thuật, và nhiều lĩnh vực khác.
Trong vật lý, phép tính hiệu thường được sử dụng để tính toán sự thay đổi của các đại lượng như vận tốc, khoảng cách, và năng lượng. Ví dụ, khi nghiên cứu chuyển động của một vật thể, các nhà vật lý sử dụng phép tính hiệu để xác định sự thay đổi vận tốc theo thời gian, từ đó đưa ra các phân tích và dự đoán chính xác về quỹ đạo và động năng của vật thể đó. Tương tự, trong các thí nghiệm liên quan đến nhiệt động lực học, phép tính hiệu giúp tính toán sự thay đổi năng lượng trong các quá trình nhiệt, từ đó giúp hiểu rõ hơn về hiệu suất và hiệu quả của các hệ thống nhiệt.
Trong kỹ thuật, phép tính hiệu được áp dụng rộng rãi để đo lường và điều chỉnh sai lệch của các máy móc và thiết bị. Một ví dụ điển hình là trong lĩnh vực cơ khí, phép tính hiệu giúp các kỹ sư xác định và điều chỉnh sai lệch trong các bộ phận máy móc để đảm bảo hoạt động chính xác và hiệu quả. Ngoài ra, trong lĩnh vực điện tử, phép tính hiệu được sử dụng để đo lường sự khác biệt giữa các tín hiệu điện, từ đó giúp tối ưu hóa hiệu suất của các mạch điện và thiết bị điện tử.
Như vậy, phép tính hiệu không chỉ là một công cụ toán học quan trọng mà còn là một phương tiện thiết yếu giúp các nhà khoa học và kỹ sư hiểu rõ hơn về sự biến đổi và khác biệt trong các hệ thống, từ đó đưa ra các giải pháp tối ưu và cải tiến các công nghệ hiện đại.
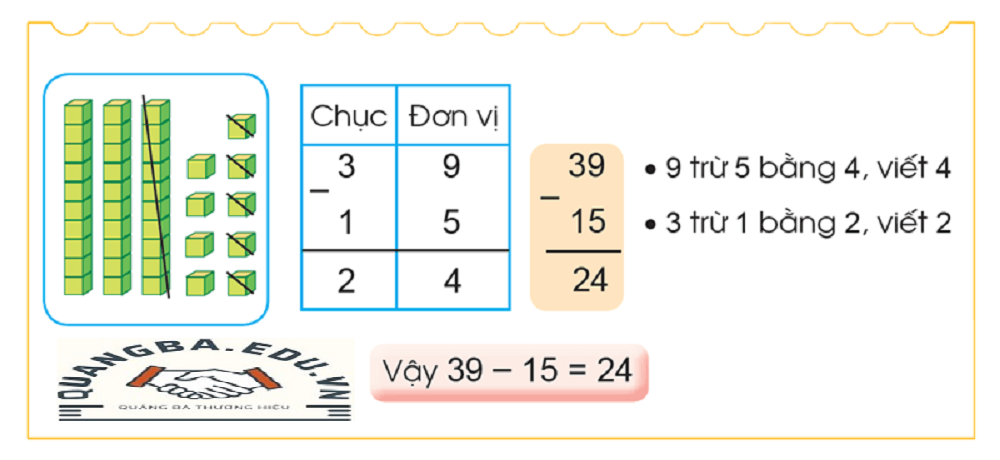
Phép tính hiệu trong toán học nâng cao
Trong toán học nâng cao, phép tính hiệu không chỉ dừng lại ở những phép toán cơ bản mà đã mở rộng sang nhiều lĩnh vực phức tạp hơn như giải tích, đại số, và xác suất thống kê. Một ví dụ điển hình của sự ứng dụng này là trong giải tích, nơi phép tính hiệu được sử dụng để tính đạo hàm và tích phân. Đạo hàm là một công cụ quan trọng giúp nghiên cứu sự thay đổi tức thời của hàm số, trong khi tích phân giúp tính toán sự tích lũy, chẳng hạn như diện tích dưới đường cong.
Trong giải tích, phép tính hiệu đóng vai trò quan trọng trong việc xác định các giới hạn và chuỗi số, điều này là nền tảng cho nhiều khái niệm phức tạp hơn như chuỗi Taylor và chuỗi Fourier. Phép tính hiệu giúp chúng ta hiểu rõ hơn về hành vi của các hàm số khi chúng tiến đến vô cùng nhỏ hoặc vô cùng lớn, điều này rất cần thiết trong nghiên cứu các hiện tượng vật lý và kỹ thuật.
Trong đại số, phép tính hiệu cũng được áp dụng để giải quyết các hệ phương trình tuyến tính và phi tuyến tính. Việc sử dụng phép tính hiệu giúp xác định các giá trị riêng và vectơ riêng của ma trận, điều này là cơ sở cho nhiều ứng dụng trong vật lý, kỹ thuật và khoa học máy tính. Phép tính hiệu còn giúp giải quyết các bài toán tối ưu hóa, nơi yêu cầu tìm giá trị cực đại hoặc cực tiểu của một hàm số.
Trong xác suất thống kê, phép tính hiệu được sử dụng để tính toán các biến ngẫu nhiên và các phân phối xác suất. Chẳng hạn, việc sử dụng phép tính hiệu để tính các hàm mật độ xác suất và hàm phân phối tích lũy giúp chúng ta hiểu rõ hơn về các hiện tượng ngẫu nhiên và dự đoán xác suất của các sự kiện. Điều này rất quan trọng trong các lĩnh vực như tài chính, bảo hiểm, và nghiên cứu khoa học.
Như vậy, phép tính hiệu trong toán học nâng cao không chỉ là một công cụ toán học cơ bản mà còn là nền tảng cho nhiều lĩnh vực nghiên cứu và ứng dụng phức tạp, giúp chúng ta hiểu rõ hơn về thế giới xung quanh.
Các phương pháp và kỹ thuật tính hiệu hiệu quả
Để thực hiện phép tính hiệu một cách hiệu quả, có nhiều phương pháp và kỹ thuật khác nhau có thể được áp dụng. Một trong những phương pháp phổ biến nhất là sử dụng các công cụ tính toán như máy tính cầm tay hoặc phần mềm tính toán chuyên dụng. Những công cụ này giúp tính toán nhanh chóng và chính xác, đồng thời giảm thiểu rủi ro sai sót do tính toán thủ công. Ngoài ra, việc sử dụng bảng tính điện tử như Microsoft Excel hay Google Sheets cũng là một lựa chọn hiệu quả, đặc biệt khi cần xử lý lượng lớn dữ liệu.
Một kỹ thuật khác là áp dụng các chiến lược tư duy như phân tích từng bước và chia nhỏ bài toán. Khi đối mặt với một bài toán phức tạp, việc chia nhỏ thành các phần nhỏ hơn và giải quyết từng phần một có thể giúp quá trình tính toán trở nên dễ dàng hơn. Phương pháp này không chỉ giúp tiết kiệm thời gian mà còn tăng độ chính xác của kết quả cuối cùng.
Hơn nữa, việc nắm vững các quy tắc và công thức toán học cơ bản cũng là một yếu tố quan trọng trong việc thực hiện phép tính hiệu một cách hiệu quả. Việc hiểu rõ các quy tắc này giúp bạn có thể áp dụng chúng một cách linh hoạt vào các tình huống khác nhau, từ đó rút ngắn thời gian tính toán và giảm thiểu sai sót.
Cuối cùng, việc thực hành thường xuyên và kiểm tra lại kết quả sau khi hoàn thành phép tính cũng là một phần không thể thiếu trong quá trình này. Điều này giúp bạn phát hiện và sửa chữa kịp thời các sai sót, đồng thời nâng cao kỹ năng tính toán của mình qua từng lần thực hiện.
Bài viết xem thêm: Thương là phép tính gì?
Kết luận và tóm tắt
Phép tính hiệu là một phần quan trọng không thể thiếu trong toán học và cuộc sống hàng ngày. Hiểu rõ về định nghĩa, tính chất, và ứng dụng của phép tính này giúp chúng ta có thể áp dụng nó một cách hiệu quả trong nhiều lĩnh vực khác nhau. Việc nắm vững các phương pháp và kỹ thuật tính hiệu cũng là một kỹ năng cần thiết để giải quyết các vấn đề toán học và thực tiễn một cách chính xác.
Trong toán học, phép tính hiệu không chỉ đơn thuần là quá trình trừ đi một số từ một số khác mà còn là nền tảng cho nhiều khái niệm và phương pháp tính toán khác. Việc hiểu rõ bản chất và cách áp dụng phép tính này giúp chúng ta dễ dàng hơn trong việc học tập và nghiên cứu các lĩnh vực khác như đại số, hình học và giải tích.