Công Thức Tính Diện Tích Tứ Giác
Công Thức Tính Diện Tích Tứ Giác – trong lĩnh vực hình học, tứ giác là một hình có bốn cạnh và bốn góc. Tứ giác là một trong những dạng hình học cơ bản và được chia thành nhiều loại khác nhau, mỗi loại mang những đặc điểm và công thức tính diện tích riêng biệt. Để hiểu rõ hơn về từng loại tứ giác và cách tính diện tích của chúng, trước hết chúng ta cần phân loại chúng. Một số loại tứ giác phổ biến bao gồm hình vuông, hình chữ nhật, hình thoi, và hình thang.
Giới Thiệu Về Tứ Giác
Hình vuông là một tứ giác có bốn cạnh bằng nhau và bốn góc vuông. Còn hình chữ nhật thì cũng có bốn góc vuông nhưng chỉ có hai cặp cạnh đối diện bằng nhau. Hình thoi là một tứ giác đặc biệt với bốn cạnh bằng nhau nhưng không nhất thiết phải có góc vuông. Trong khi đó, hình thang có một cặp cạnh đối diện song song và không yêu cầu các cạnh khác phải bằng nhau hoặc có góc vuông.
Bài viết liên quan: Khối Lập Phương Là Gì?
Việc phân biệt các loại tứ giác này không chỉ giúp chúng ta nhận biết hình dạng mà còn hỗ trợ trong quá trình tính toán diện tích của chúng. Mỗi loại tứ giác sẽ có công thức tính diện tích riêng, và việc biết được đặc điểm của từng loại sẽ giúp cho việc áp dụng các công thức này trở nên dễ dàng và chính xác hơn. Bên cạnh đó, việc hiểu rõ về tứ giác cũng là nền tảng quan trọng cho việc nghiên cứu các dạng hình học phức tạp hơn trong tương lai.
Trong bài viết này, chúng tôi sẽ cung cấp thông tin chi tiết về cách tính diện tích của các loại tứ giác phổ biến, giúp bạn có cái nhìn tổng quan và ứng dụng hiệu quả trong học tập cũng như công việc thực tế.
Công Thức Tổng Quát Tính Diện Tích Tứ Giác
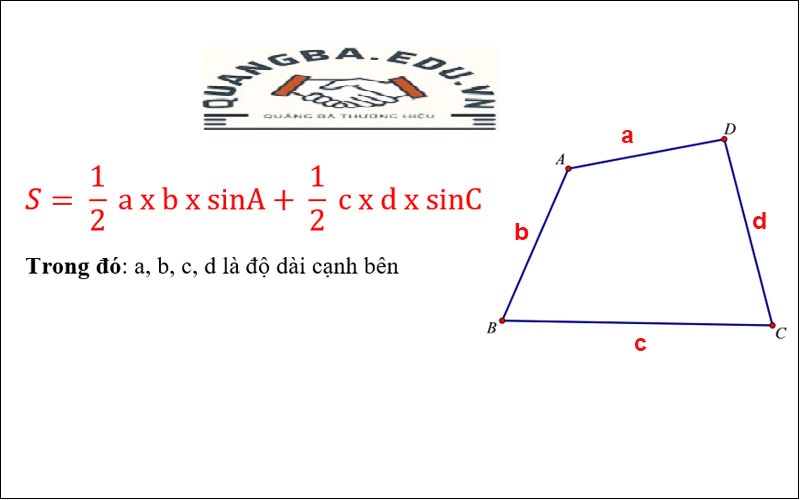
Diện tích của một tứ giác bất kỳ có thể được tính bằng nhiều cách khác nhau, phụ thuộc vào hình dạng và đặc tính của nó. Một trong những công thức tổng quát nhất để tính diện tích tứ giác là sử dụng công thức Brahmagupta. Công thức này yêu cầu biết độ dài các cạnh và các góc của tứ giác. Đối với tứ giác nội tiếp, diện tích có thể được tính bằng công thức:
S = √((s-a)(s-b)(s-c)(s-d) – abcd * cos²(θ/2))
Trong đó, s là nửa chu vi của tứ giác, a, b, c, d là độ dài các cạnh, và θ là tổng hai góc đối diện. Công thức này phức tạp hơn so với các công thức cho các loại tứ giác đặc biệt như hình thang và hình bình hành.
Với hình thang, công thức tính diện tích đơn giản hơn nhiều. Diện tích của hình thang được tính bằng:
S = ((a + b) * h) / 2
Trong đó, a và b là độ dài hai đáy, và h là chiều cao giữa hai đáy.
Đối với hình bình hành, công thức tính diện tích cũng khá đơn giản. Diện tích của hình bình hành được tính bằng:
S = a * h
Trong đó, a là độ dài một cạnh đáy và h là chiều cao tương ứng.
Việc nắm vững những công thức này giúp bạn dễ dàng tính toán diện tích của các loại tứ giác khác nhau một cách chính xác và hiệu quả. Mỗi công thức đều có ứng dụng riêng, phụ thuộc vào thông tin mà bạn có về tứ giác cần tính diện tích.
Tính Diện Tích Hình Vuông
Hình vuông là một loại tứ giác đặc biệt với bốn cạnh đều nhau và bốn góc vuông. Điều này có nghĩa là tất cả các cạnh của hình vuông đều có cùng chiều dài, và mỗi góc của nó đều là 90 độ. Công thức tính diện tích hình vuông cực kỳ đơn giản và dễ nhớ: Diện tích = cạnh * cạnh.
Lấy ví dụ minh họa, giả sử bạn có một hình vuông với chiều dài cạnh là 5 cm. Để tính diện tích của hình vuông này, bạn chỉ cần nhân chiều dài của một cạnh với chính nó. Áp dụng công thức, ta có:
Diện tích = cạnh * cạnh = 5 cm * 5 cm = 25 cm²
Qua ví dụ này, ta có thể thấy rằng việc tính diện tích của hình vuông là một quy trình đơn giản nhưng rất hữu ích trong nhiều tình huống thực tế. Bất kể cạnh của hình vuông có chiều dài bao nhiêu, chỉ cần áp dụng công thức trên, bạn có thể nhanh chóng xác định diện tích của nó. Điều này đặc biệt hữu dụng trong các lĩnh vực như kiến trúc, xây dựng và thiết kế nội thất, nơi mà việc tính toán diện tích là rất quan trọng.
Hãy xem một ví dụ khác để làm rõ hơn. Nếu bạn có một hình vuông với cạnh dài 8 m, diện tích của nó sẽ là:
Diện tích = cạnh * cạnh = 8 m * 8 m = 64 m²
Như vậy, chỉ cần nhớ công thức đơn giản này, bạn có thể dễ dàng tính toán diện tích của bất kỳ hình vuông nào. Điều này giúp tiết kiệm thời gian và công sức trong quá trình làm việc hay học tập, đặc biệt là khi bạn cần đưa ra các quyết định nhanh chóng dựa trên diện tích của các không gian hình vuông.
Tính Diện Tích Hình Chữ Nhật
Hình chữ nhật là một hình học cơ bản với hai cặp cạnh đối song song và bằng nhau, cùng bốn góc vuông. Để tính diện tích hình chữ nhật, chúng ta sử dụng công thức:
Diện tích = chiều dài * chiều rộng
Điều này có nghĩa rằng diện tích của hình chữ nhật được xác định bằng cách nhân chiều dài của nó với chiều rộng. Công thức này rất đơn giản và dễ hiểu, nhưng để áp dụng nó một cách hiệu quả, chúng ta cần hiểu rõ các yếu tố liên quan.
Hãy cùng xem xét một ví dụ thực tế để minh họa cách thức tính diện tích hình chữ nhật. Giả sử chúng ta có một hình chữ nhật với chiều dài là 8 mét và chiều rộng là 5 mét. Để tính diện tích của hình chữ nhật này, chúng ta sẽ nhân chiều dài với chiều rộng:
Diện tích = 8 mét * 5 mét = 40 mét vuông
Do đó, diện tích của hình chữ nhật này là 40 mét vuông. Điều này có thể áp dụng cho bất kỳ hình chữ nhật nào, miễn là chúng ta biết chiều dài và chiều rộng của nó.
Một ví dụ khác là nếu chúng ta có một hình chữ nhật với chiều dài là 12 mét và chiều rộng là 7 mét. Khi áp dụng công thức tính diện tích, chúng ta sẽ có:
Diện tích = 12 mét * 7 mét = 84 mét vuông
Trong thực tế, việc tính diện tích hình chữ nhật rất hữu ích trong nhiều lĩnh vực, chẳng hạn như xây dựng, nội thất, và quy hoạch không gian. Bằng cách sử dụng công thức đơn giản này, chúng ta có thể dễ dàng xác định diện tích của bất kỳ hình chữ nhật nào, từ đó hỗ trợ cho việc lập kế hoạch và triển khai các dự án một cách hiệu quả.
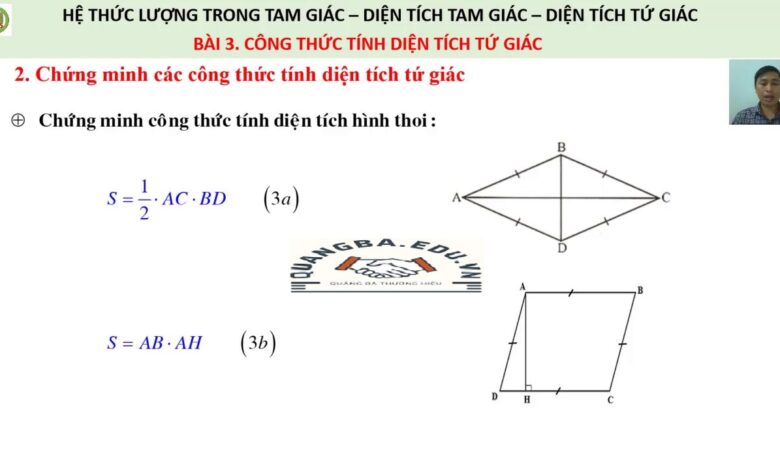
Tính Diện Tích Hình Thoi
Hình thoi là một loại tứ giác đặc biệt, nơi bốn cạnh có độ dài bằng nhau nhưng các góc không nhất thiết phải bằng 90 độ. Để tính diện tích hình thoi, một công thức phổ biến và dễ nhớ là sử dụng độ dài của hai đường chéo. Công thức này là:
Diện tích = (đường chéo dài * đường chéo ngắn) / 2
Để minh họa công thức này, hãy xem xét một số ví dụ cụ thể. Giả sử chúng ta có một hình thoi với các đường chéo dài 10 cm và 8 cm. Áp dụng công thức trên, diện tích của hình thoi sẽ là:
Diện tích = (10 cm * 8 cm) / 2 = 40 cm²
Trong trường hợp khác, nếu đường chéo dài là 12 cm và đường chéo ngắn là 5 cm, diện tích hình thoi sẽ được tính như sau:
Diện tích = (12 cm * 5 cm) / 2 = 30 cm²
Việc sử dụng công thức này không chỉ nhanh chóng mà còn rất hiệu quả, đặc biệt khi bạn biết trước độ dài của các đường chéo. Điều này giúp tiết kiệm thời gian và đảm bảo tính chính xác. Thực tế, công thức này có thể áp dụng cho mọi hình thoi, bất kể kích thước và hình dạng cụ thể của nó.
Hình thoi không chỉ xuất hiện trong hình học lý thuyết mà còn trong nhiều ứng dụng thực tế như kiến trúc, trang trí và nghệ thuật. Hiểu rõ cách tính diện tích hình thoi giúp chúng ta có cái nhìn sâu hơn về hình học và áp dụng nó vào những tình huống cụ thể trong cuộc sống hàng ngày.
Tính Diện Tích Hình Thang
Hình thang là một loại tứ giác đặc biệt với hai cạnh đối song song. Để tính diện tích hình thang, ta sử dụng công thức cơ bản sau: Diện tích = (đáy lớn + đáy nhỏ) * chiều cao / 2. Công thức này giúp xác định diện tích của hình thang một cách dễ dàng và nhanh chóng, khi biết các kích thước cần thiết.
Ví dụ, giả sử chúng ta có một hình thang với đáy lớn là 8 cm, đáy nhỏ là 5 cm, và chiều cao là 4 cm. Áp dụng công thức trên, ta có:
Diện tích = (8 cm + 5 cm) * 4 cm / 2 = 13 cm * 4 cm / 2 = 26 cm²
Như vậy, diện tích của hình thang này là 26 cm². Việc xác định các thành phần như đáy lớn, đáy nhỏ và chiều cao là rất quan trọng để đảm bảo tính chính xác của kết quả.
Để giúp người đọc hiểu rõ hơn, hãy xem một ví dụ khác. Giả sử một hình thang có đáy lớn là 10 cm, đáy nhỏ là 6 cm và chiều cao là 5 cm. Áp dụng công thức:
Diện tích = (10 cm + 6 cm) * 5 cm / 2 = 16 cm * 5 cm / 2 = 40 cm²
Trong trường hợp này, diện tích của hình thang là 40 cm². Những ví dụ này minh họa việc áp dụng công thức diện tích hình thang vào thực tế.
Để củng cố kiến thức, người đọc có thể thực hành thêm bằng cách tự giải các bài tập tương tự. Ví dụ: Tính diện tích của một hình thang với đáy lớn là 12 cm, đáy nhỏ là 8 cm và chiều cao là 6 cm. Áp dụng công thức trên, người đọc sẽ dễ dàng tìm ra diện tích của hình thang đó.
Ứng Dụng Công Thức Brahmagupta
Công thức Brahmagupta là một công cụ toán học quan trọng được sử dụng để tính diện tích của một tứ giác nội tiếp trong một đường tròn. Công thức này được biểu diễn dưới dạng: Diện tích = √((s-a)(s-b)(s-c)(s-d)), trong đó s là nửa chu vi và a, b, c, d là các cạnh của tứ giác. Để áp dụng công thức này, trước tiên chúng ta cần xác định giá trị của s, được tính bằng công thức s = (a + b + c + d) / 2.
Ví dụ minh họa sẽ giúp làm rõ cách sử dụng công thức Brahmagupta. Giả sử chúng ta có một tứ giác nội tiếp với các cạnh lần lượt là a = 5, b = 6, c = 7 và d = 8. Đầu tiên, chúng ta tính nửa chu vi s:
s = (a + b + c + d) / 2 = (5 + 6 + 7 + 8) / 2 = 13
Sau khi có giá trị s, chúng ta áp dụng công thức Brahmagupta:
Diện tích = √((s-a)(s-b)(s-c)(s-d)) = √((13-5)(13-6)(13-7)(13-8)) = √(8 * 7 * 6 * 5) = √1680 ≈ 40,99
Bài viết xem thêm: Hoán Dụ Là Gì
Như vậy, diện tích của tứ giác nội tiếp này là khoảng 40,99 đơn vị vuông. Công thức Brahmagupta không chỉ giúp tính toán chính xác diện tích của các tứ giác nội tiếp mà còn là một minh chứng cho sự kết nối giữa hình học và đại số. Nhờ vào công thức này, những bài toán liên quan đến diện tích tứ giác trở nên dễ dàng và trực quan hơn.
Trong thực tế, công thức Brahmagupta có thể được ứng dụng trong nhiều lĩnh vực khác nhau, từ toán học lý thuyết cho đến các ứng dụng thực tế trong kiến trúc, kỹ thuật và thiết kế. Việc hiểu rõ và biết cách sử dụng công thức này sẽ mang lại nhiều lợi ích, giúp giải quyết các bài toán một cách nhanh chóng và hiệu quả.




