Thể tích hình hộp chữ nhật

Hình hộp chữ nhật là một trong những hình học cơ bản và phổ biến trong toán học cũng như trong các ứng dụng thực tế. Được định nghĩa là một hình không gian ba chiều với sáu mặt đều là các hình chữ nhật, hình hộp chữ nhật có thể dễ dàng nhận diện và thường xuyên gặp trong cuộc sống hàng ngày, chẳng hạn như trong các hộp đóng gói, các khối xây dựng, và nhiều vật thể khác.
Giới thiệu về hình hộp chữ nhật
Mỗi hình hộp chữ nhật được xác định bởi ba kích thước chính: chiều dài, chiều rộng và chiều cao. Các mặt đối diện của hình hộp chữ nhật là những hình chữ nhật có diện tích bằng nhau. Điều này làm cho hình hộp chữ nhật có các tính chất hình học độc đáo, ví dụ như số cạnh bằng nhau và các góc đều là góc vuông. Việc nắm bắt các đặc điểm này giúp việc tính toán trở nên dễ dàng và chính xác hơn.
Bài viết liên quan: Hình Tam Giác
Việc tính toán thể tích của hình hộp chữ nhật là một kỹ năng quan trọng không chỉ trong toán học mà còn trong nhiều lĩnh vực khác như kỹ thuật, kiến trúc, và quản lý không gian. Thể tích của hình hộp chữ nhật được tính bằng công thức đơn giản là tích của chiều dài, chiều rộng và chiều cao. Công thức này giúp đánh giá không gian bên trong của hộp, từ đó áp dụng cho việc thiết kế, xây dựng và lưu trữ hiệu quả.
Bằng cách hiểu rõ về hình hộp chữ nhật và cách tính thể tích của nó, chúng ta có thể ứng dụng vào nhiều tình huống thực tế, từ việc tính toán dung tích của các container, tối ưu hóa không gian lưu trữ cho đến việc quản lý vật liệu xây dựng. Chính vì vậy, kiến thức về hình hộp chữ nhật và thể tích của nó không chỉ mang tính học thuật mà còn có giá trị thực tiễn cao.
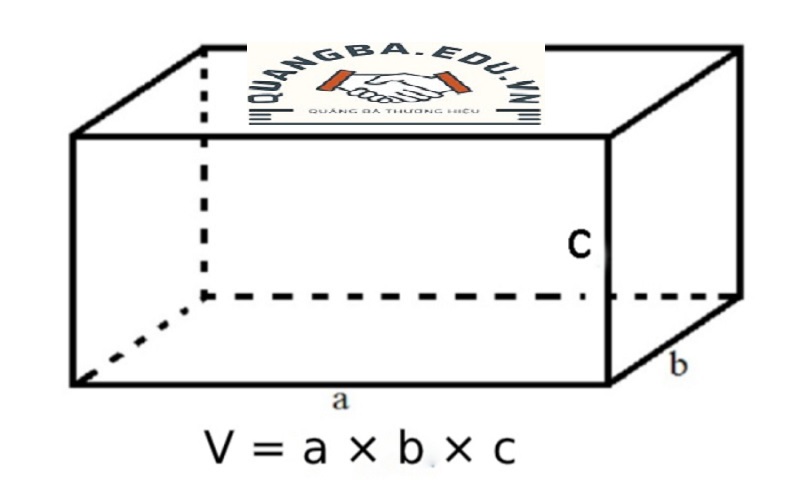
Công thức tính thể tích hình hộp chữ nhật
Để tính thể tích của một hình hộp chữ nhật, chúng ta sử dụng công thức đơn giản nhưng hiệu quả sau:
V = l * w * h
Trong đó:
– V là thể tích của hình hộp chữ nhật.
– l là chiều dài của hình hộp chữ nhật.
– w là chiều rộng của hình hộp chữ nhật.
– h là chiều cao của hình hộp chữ nhật.
Công thức này cho phép chúng ta tính toán dễ dàng bằng cách nhân ba kích thước chính của hình hộp chữ nhật với nhau. Để áp dụng công thức này, cần đo chính xác chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật.
Ví dụ, nếu chúng ta có một hình hộp chữ nhật với chiều dài là 5 cm, chiều rộng là 3 cm và chiều cao là 4 cm, thể tích của nó sẽ được tính như sau:
V = 5 cm * 3 cm * 4 cm = 60 cm³
Đây là một công thức cơ bản nhưng chính xác và được sử dụng rộng rãi trong nhiều lĩnh vực như xây dựng, đóng gói và sản xuất. Việc hiểu và áp dụng đúng công thức này không chỉ giúp chúng ta tính toán chính xác thể tích của các vật thể hình hộp chữ nhật mà còn cung cấp nền tảng kiến thức cơ bản cho những phép tính phức tạp hơn trong tương lai.
Việc nắm vững công thức tính thể tích hình hộp chữ nhật là bước quan trọng giúp chúng ta có thể ứng dụng vào thực tế một cách hiệu quả, từ việc xác định dung tích chứa bên trong một chiếc hộp đến việc tính toán không gian lưu trữ trong các kho hàng hay các dự án xây dựng.
Các đơn vị đo lường thể tích
Trong toán học và khoa học, thể tích thường được đo lường bằng các đơn vị khối như mét khối (m³), centimet khối (cm³), và lít. Hiểu rõ về các đơn vị đo lường này và cách chuyển đổi giữa chúng là rất quan trọng trong nhiều lĩnh vực khác nhau.
Mét khối (m³) là đơn vị tiêu chuẩn trong Hệ đo lường quốc tế (SI) để đo lường thể tích. Một mét khối tương đương với thể tích của một khối lập phương có cạnh dài một mét. Đơn vị này thường được sử dụng trong các tình huống yêu cầu đo lường thể tích lớn, chẳng hạn như trong xây dựng, kỹ thuật và quản lý tài nguyên thiên nhiên.
Centimet khối (cm³) là một đơn vị nhỏ hơn, thích hợp để đo các thể tích nhỏ. Một centimet khối tương đương với thể tích của một khối lập phương có cạnh dài một centimet. Trong thực tế, 1 m³ bằng 1.000.000 cm³. Đơn vị này thường được sử dụng trong các lĩnh vực như hóa học, vật lý, và y học, nơi mà các phép đo yêu cầu độ chính xác cao và thể tích nhỏ.
Lít là một đơn vị đo lường thể tích phổ biến khác, thường được sử dụng để đo chất lỏng. Một lít tương đương với 1 dm³ (một decimet khối), và có thể chuyển đổi thành 1.000 cm³ hoặc 0,001 m³. Đơn vị lít thường được sử dụng trong đời sống hàng ngày, từ đo lường thể tích nước uống đến nhiên liệu và các chất lỏng khác.
Cách chuyển đổi giữa các đơn vị này rất quan trọng. Ví dụ, để chuyển đổi từ mét khối sang lít, ta nhân với 1.000 (1 m³ = 1.000 lít). Tương tự, để chuyển đổi từ centimet khối sang lít, ta chia cho 1.000 (1.000 cm³ = 1 lít). Hiểu rõ các đơn vị đo lường này giúp đảm bảo tính chính xác và hiệu quả trong công việc cũng như trong cuộc sống hàng ngày.
Ví dụ minh họa thực tế
Để làm rõ quá trình tính toán thể tích hình hộp chữ nhật, chúng ta sẽ cùng đi qua một vài ví dụ minh họa thực tế. Những ví dụ này sẽ giúp bạn hiểu rõ hơn cách đo lường các kích thước và áp dụng công thức tính thể tích một cách chính xác.
Ví dụ đầu tiên, giả sử chúng ta có một hình hộp chữ nhật với các kích thước đo được như sau: chiều dài 5 mét, chiều rộng 3 mét và chiều cao 2 mét. Để tính thể tích, chúng ta áp dụng công thức V = l × w × h, trong đó V là thể tích, l là chiều dài, w là chiều rộng và h là chiều cao. Vậy, thể tích của hình hộp này sẽ là:
V = 5 m × 3 m × 2 m = 30 mét khối.
Trong một ví dụ khác, giả sử chúng ta có một hình hộp chữ nhật nhỏ hơn với chiều dài 2.5 mét, chiều rộng 1.8 mét và chiều cao 1.2 mét. Sử dụng cùng công thức trên, chúng ta có:
V = 2.5 m × 1.8 m × 1.2 m = 5.4 mét khối.
Cuối cùng, hãy xem xét một ứng dụng thực tế khác. Giả sử bạn cần tính thể tích của một bể chứa nước hình hộp chữ nhật có chiều dài 10 mét, chiều rộng 4 mét và chiều cao 3.5 mét. Áp dụng công thức tính thể tích:
V = 10 m × 4 m × 3.5 m = 140 mét khối.
Những ví dụ này minh họa rõ ràng cách đo lường các kích thước và áp dụng công thức tính thể tích hình hộp chữ nhật. Việc hiểu và thực hành thông qua các ví dụ thực tế sẽ giúp bạn dễ dàng hơn trong việc áp dụng kiến thức này vào các tình huống thực tế, từ việc thiết kế các cấu trúc xây dựng đến các ứng dụng trong công nghiệp và đời sống hàng ngày.
Ứng dụng của thể tích hình hộp chữ nhật trong đời sống
Thể tích hình hộp chữ nhật là một khái niệm toán học cơ bản nhưng có rất nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Trong lĩnh vực xây dựng, việc tính toán thể tích hình hộp chữ nhật giúp các kỹ sư và kiến trúc sư xác định chính xác lượng vật liệu cần thiết, chẳng hạn như bê tông, gạch, và thép, để xây dựng các công trình. Điều này không chỉ đảm bảo tính chính xác và an toàn của công trình mà còn giúp tiết kiệm chi phí và thời gian.
Trong ngành đóng gói, thể tích hình hộp chữ nhật là tiêu chí quan trọng để thiết kế các bao bì sản phẩm. Việc tính toán chính xác thể tích giúp các nhà sản xuất tối ưu hóa không gian, giảm thiểu chi phí vận chuyển và lưu kho. Chẳng hạn, việc đóng gói hàng hóa trong các thùng carton có thể tích hình hộp chữ nhật giúp tận dụng tối đa không gian trong kho hoặc trên phương tiện vận chuyển, từ đó nâng cao hiệu suất kinh tế.
Thiết kế nội thất cũng là một lĩnh vực mà thể tích hình hộp chữ nhật được áp dụng rộng rãi. Các nhà thiết kế sử dụng khái niệm này để tạo ra các món đồ nội thất như tủ, bàn, và kệ sao cho phù hợp với không gian sống. Việc tính toán thể tích giúp đảm bảo rằng các món đồ này không chỉ đẹp mắt mà còn tiện dụng, phù hợp với kích thước và diện tích của căn phòng.
Thể tích hình hộp chữ nhật còn được ứng dụng trong nhiều lĩnh vực khác như y tế, nông nghiệp, và logistics. Ví dụ, trong y tế, thể tích hình hộp chữ nhật được dùng để thiết kế các thiết bị y tế như máy chụp X-quang, tủ lạnh bảo quản thuốc. Trong nông nghiệp, nó giúp tính toán thể tích các silo chứa hạt, kho chứa thức ăn gia súc. Trong logistics, thể tích hình hộp chữ nhật giúp tối ưu hóa không gian trong các container vận chuyển hàng hóa.
Các lỗi thường gặp khi tính thể tích
Trong quá trình tính toán thể tích hình hộp chữ nhật, một số lỗi phổ biến mà nhiều người thường gặp phải có thể ảnh hưởng đến kết quả cuối cùng. Hiểu rõ và tránh những lỗi này sẽ giúp bạn có được kết quả chính xác hơn.
Đầu tiên, nhầm lẫn đơn vị đo lường là một lỗi khá phổ biến. Khi đo các kích thước của hình hộp chữ nhật, việc sử dụng các đơn vị đo lường khác nhau mà không quy đổi về cùng một đơn vị chuẩn sẽ dẫn đến kết quả sai lệch. Ví dụ, nếu bạn đo chiều dài bằng mét nhưng chiều rộng lại đo bằng centimet, thể tích tính ra sẽ không chính xác. Vì vậy, hãy đảm bảo tất cả các đơn vị đo lường đều đồng nhất trước khi thực hiện tính toán.
Thứ hai, sai số trong việc đo đạc các kích thước cũng là một nguyên nhân dẫn đến kết quả không chính xác. Để tính toán thể tích chính xác, các giá trị chiều dài, chiều rộng và chiều cao cần được đo đạc cẩn thận và chính xác. Sử dụng các công cụ đo lường có độ chính xác cao và kiểm tra lại các kết quả đo để đảm bảo không có sai sót.
Cuối cùng, quên áp dụng công thức đúng cách là một lỗi mà nhiều người mắc phải. Công thức tính thể tích hình hộp chữ nhật rất đơn giản: V = Dài x Rộng x Cao. Tuy nhiên, nếu không chú ý và áp dụng sai các bước trong công thức, kết quả sẽ không đúng. Hãy chắc chắn rằng bạn đã hiểu rõ công thức và áp dụng đúng cách.
Việc nhận biết và khắc phục những lỗi này sẽ giúp bạn tính toán thể tích hình hộp chữ nhật một cách chính xác và hiệu quả hơn. Hãy luôn chú ý kiểm tra và đối chiếu các bước thực hiện để đảm bảo kết quả cuối cùng là chính xác nhất.
Các bài tập thực hành
Để giúp người đọc nắm vững hơn về cách tính thể tích hình hộp chữ nhật, chúng tôi sẽ cung cấp một số bài tập thực hành. Mỗi bài tập không chỉ giúp củng cố kiến thức mà còn rèn luyện kỹ năng tính toán.
Bài tập 1: Một hình hộp chữ nhật có chiều dài 5 cm, chiều rộng 3 cm và chiều cao 4 cm. Tính thể tích của hình hộp chữ nhật này.
Giải:
Thể tích của hình hộp chữ nhật được tính bằng công thức:
V = dài x rộng x cao
Thay các giá trị đã cho vào công thức:
V = 5 cm x 3 cm x 4 cm = 60 cm3
Vậy thể tích của hình hộp chữ nhật là 60 cm3.
Bài tập 2: Một hộp chứa đồ có chiều dài 10 cm, chiều rộng 6 cm và chiều cao 8 cm. Tính thể tích của hộp chứa đồ này.
Giải:
Sử dụng công thức tính thể tích:
V = dài x rộng x cao
Thay các giá trị đã cho vào công thức:
V = 10 cm x 6 cm x 8 cm = 480 cm3
Vậy thể tích của hộp chứa đồ là 480 cm3.
Bài tập 3: Một bể cá có chiều dài 15 cm, chiều rộng 10 cm và chiều cao 12 cm. Tính thể tích của bể cá này.
Giải:
Áp dụng công thức tính thể tích:
V = dài x rộng x cao
Thay các giá trị đã cho vào công thức:
V = 15 cm x 10 cm x 12 cm = 1800 cm3
Vậy thể tích của bể cá là 1800 cm3.
Qua các bài tập trên, người đọc có thể dễ dàng nắm rõ cách tính thể tích hình hộp chữ nhật. Hãy thử tự mình giải các bài tập tương tự để kiểm tra và củng cố kiến thức đã học.
Bài viết xem thêm: 1ha bằng bao nhiêu m2
Kết luận và tài liệu
Tính toán thể tích hình hộp chữ nhật là một kỹ năng quan trọng trong nhiều lĩnh vực, từ giáo dục đến công việc thực tế hàng ngày. Bài viết đã cung cấp một hướng dẫn chi tiết về cách tính thể tích hình hộp chữ nhật, bao gồm các bước cơ bản và những lưu ý quan trọng. Việc hiểu và áp dụng đúng các kiến thức này không chỉ giúp bạn thực hiện các bài tập toán học một cách chính xác mà còn có thể áp dụng trong các tình huống thực tế như thiết kế, xây dựng và quản lý không gian.
Để tính thể tích hình hộp chữ nhật, bạn cần nhân ba cạnh của nó với nhau: chiều dài, chiều rộng và chiều cao. Công thức này tuy đơn giản nhưng đòi hỏi sự chính xác trong quá trình đo lường và tính toán. Việc sử dụng đúng đơn vị đo lường và kiểm tra lại các phép tính là rất quan trọng để đảm bảo kết quả cuối cùng là chính xác.