Công Thức Tính Diện Tích Hình Tròn
Công Thức Tính Diện Tích Hình Tròn – hình tròn là một trong những hình học cơ bản và quan trọng nhất trong toán học. Nó không chỉ xuất hiện trong sách giáo khoa mà còn hiện diện trong cuộc sống hàng ngày từ những vật thể tròn như đồng hồ, bánh xe, đến các thiết kế kiến trúc. Hiểu rõ về hình tròn và cách tính diện tích của nó là nền tảng để tiến xa hơn trong nhiều lĩnh vực. Bài viết này sẽ giới thiệu chi tiết về công thức tính diện tích hình tròn, cách áp dụng, và những ví dụ minh họa cụ thể.
Định nghĩa và các thành phần của hình tròn
Hình tròn là tập hợp tất cả các điểm nằm trên một mặt phẳng và cách đều một điểm cố định gọi là tâm. Khoảng cách từ tâm đến các điểm trên hình tròn được gọi là bán kính. Một số thành phần quan trọng của hình tròn bao gồm:
- Tâm: Là điểm cố định mà tất cả các điểm trên hình tròn cách đều.
- Bán kính (r): Là khoảng cách từ tâm đến một điểm bất kỳ trên hình tròn.
- Đường kính (d): Là đoạn thẳng đi qua tâm và nối hai điểm trên hình tròn. Đường kính gấp đôi bán kính (d = 2r).
- Chu vi (C): Là chiều dài đường biên của hình tròn.
- Diện tích (A): Là toàn bộ vùng mặt phẳng nằm bên trong đường tròn.
Bài viết liên quan: Sinh viên năm cuối tiếng Anh là gì?
Công thức tính diện tích hình tròn
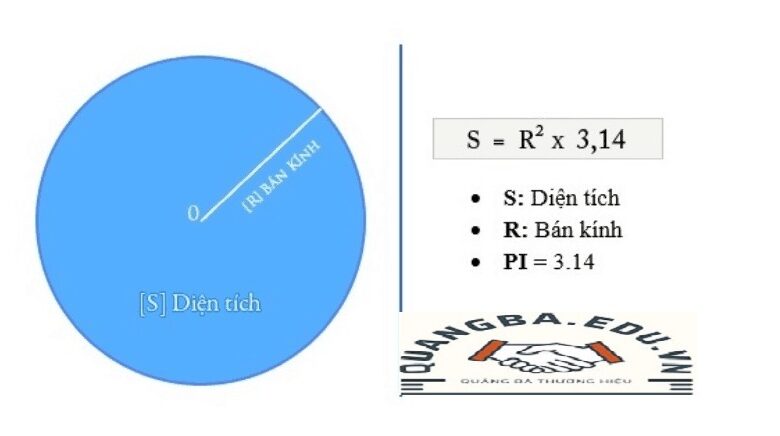
Diện tích của hình tròn được tính bằng công thức:
A=πr2A = \pi r^2A=πr2
Trong đó:
- AAA là diện tích hình tròn.
- rrr là bán kính của hình tròn.
- π\piπ (pi) là một hằng số toán học, xấp xỉ bằng 3.14159.
Giải thích công thức
Công thức diện tích hình tròn A=πr2A = \pi r^2A=πr2 được suy ra từ việc tích hợp toàn bộ diện tích của các vòng tròn nhỏ tạo thành hình tròn. Một cách khác để hiểu công thức này là từ việc chia hình tròn thành các mảnh nhỏ và xếp chúng thành hình chữ nhật. Diện tích của hình chữ nhật này chính là diện tích của hình tròn ban đầu.
Ví dụ minh họa
Ví dụ 1:
Tính diện tích của một hình tròn có bán kính 5 cm.
Áp dụng công thức:
A=πr2A = \pi r^2A=πr2 A=π×52A = \pi \times 5^2A=π×52 A=π×25A = \pi \times 25A=π×25 A≈3.14159×25A \approx 3.14159 \times 25A≈3.14159×25 A≈78.54 cm2A \approx 78.54 \, \text{cm}^2A≈78.54cm2
Vậy, diện tích của hình tròn có bán kính 5 cm là khoảng 78.54 cm².
Ví dụ 2:
Tính diện tích của một hình tròn có đường kính 10 m.
Trước hết, tính bán kính:
r=d2=102=5 mr = \frac{d}{2} = \frac{10}{2} = 5 \, \text{m}r=2d=210=5m
Áp dụng công thức:
A=πr2A = \pi r^2A=πr2 A=π×52A = \pi \times 5^2A=π×52 A=π×25A = \pi \times 25A=π×25 A≈3.14159×25A \approx 3.14159 \times 25A≈3.14159×25 A≈78.54 m2A \approx 78.54 \, \text{m}^2A≈78.54m2
Vậy, diện tích của hình tròn có đường kính 10 m là khoảng 78.54 m².
Ứng dụng của công thức tính diện tích hình tròn
Công thức tính diện tích hình tròn được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau:
- Kiến trúc và xây dựng: Đo lường và tính toán diện tích mặt bằng, mặt sân, các cấu trúc tròn như cột, mái vòm.
- Thiết kế: Trong thiết kế nội thất và ngoại thất, công thức này giúp tính toán không gian, bố trí đồ vật.
- Khoa học và kỹ thuật: Ứng dụng trong việc đo lường các bề mặt tròn, tính toán tiết diện của các ống, trục, và nhiều vật thể khác.
- Đời sống hàng ngày: Tính diện tích của các vật thể tròn như bánh, đồng hồ, đĩa…

Bài tập vận dụng
Bài tập 1: Tính diện tích của hình tròn có bán kính 7 cm.
Bài tập 2: Một bể bơi hình tròn có đường kính 14 m. Tính diện tích mặt nước của bể bơi.
Bài tập 3: Một đĩa tròn có chu vi 31.4 cm. Tính diện tích của đĩa.
Lời giải:
Bài tập 1:
Áp dụng công thức:
A=πr2A = \pi r^2A=πr2 A=π×72A = \pi \times 7^2A=π×72 A=π×49A = \pi \times 49A=π×49 A≈3.14159×49A \approx 3.14159 \times 49A≈3.14159×49 A≈153.94 cm2A \approx 153.94 \, \text{cm}^2A≈153.94cm2
Vậy, diện tích của hình tròn có bán kính 7 cm là khoảng 153.94 cm².
Bài tập 2:
Tính bán kính:
r=d2=142=7 mr = \frac{d}{2} = \frac{14}{2} = 7 \, \text{m}r=2d=214=7m
Áp dụng công thức:
A=πr2A = \pi r^2A=πr2 A=π×72A = \pi \times 7^2A=π×72 A=π×49A = \pi \times 49A=π×49 A≈3.14159×49A \approx 3.14159 \times 49A≈3.14159×49 A≈153.94 m2A \approx 153.94 \, \text{m}^2A≈153.94m2
Vậy, diện tích mặt nước của bể bơi là khoảng 153.94 m².
Bài tập 3:
Tính bán kính từ chu vi:
C=2πrC = 2\pi rC=2πr 31.4=2πr31.4 = 2\pi r31.4=2πr r=31.42πr = \frac{31.4}{2\pi}r=2π31.4 r≈31.46.28318r \approx \frac{31.4}{6.28318}r≈6.2831831.4 r≈5 cmr \approx 5 \, \text{cm}r≈5cm
Áp dụng công thức:
A=πr2A = \pi r^2A=πr2 A=π×52A = \pi \times 5^2A=π×52 A=π×25A = \pi \times 25A=π×25 A≈3.14159×25A \approx 3.14159 \times 25A≈3.14159×25 A≈78.54 cm2A \approx 78.54 \, \text{cm}^2A≈78.54cm2
Vậy, diện tích của đĩa là khoảng 78.54 cm².
Bài viết xem thêm: Cách Tính Diện Tích Hình Thang Cân
Kết luận
Hiểu và áp dụng đúng công thức tính diện tích hình tròn giúp chúng ta giải quyết nhiều bài toán thực tế và ứng dụng trong nhiều lĩnh vực khác nhau. Việc nắm vững kiến thức này là bước đệm quan trọng để tiếp tục học tập và làm việc hiệu quả trong toán học và các ngành khoa học kỹ thuật khác. Hy vọng bài viết này đã giúp bạn nắm vững cách tính diện tích hình tròn và tự tin áp dụng vào các bài toán và tình huống thực tế. Chúc bạn học tốt và thành công!