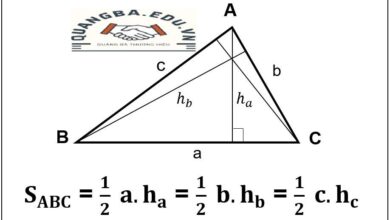
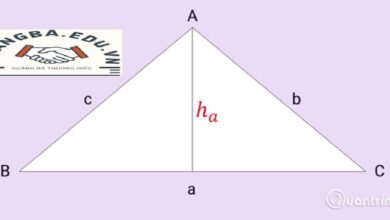
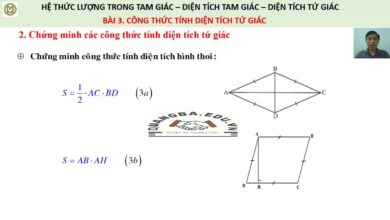
Cách Tính Diện Tích Hình Thang Cân
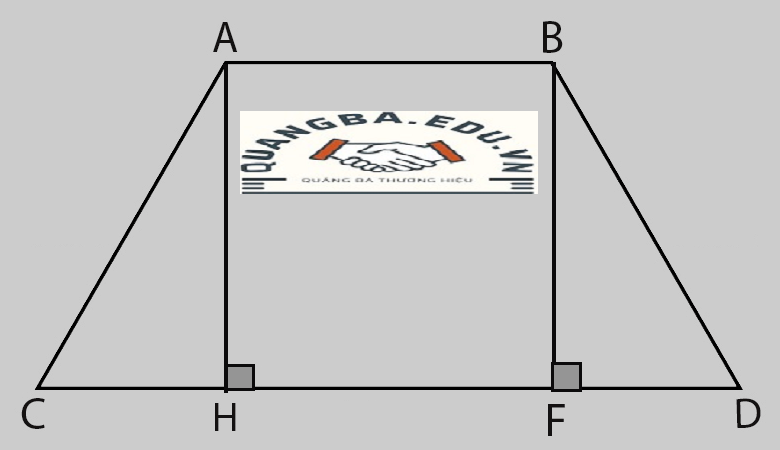
Cách Tính Diện Tích Hình Thang Cân – Hình thang cân là một hình học đặc biệt trong hình học phẳng, có hai cạnh đáy song song và hai cạnh bên bằng nhau. Đây là một trong những hình học thường gặp và việc tính diện tích của nó có thể được áp dụng trong nhiều lĩnh vực khác nhau từ toán học cơ bản đến ứng dụng thực tiễn trong xây dựng, thiết kế, và nhiều lĩnh vực khác. Bài viết này sẽ hướng dẫn bạn cách tính diện tích hình thang cân một cách chi tiết và dễ hiểu.
Định nghĩa và đặc điểm của hình thang cân
Hình thang cân là một hình thang có hai cạnh bên bằng nhau và hai cạnh đáy song song. Điều này làm cho hai góc kề một cạnh đáy cũng bằng nhau. Nếu gọi hai cạnh đáy là aaa và bbb (với a>ba > ba>b), và hai cạnh bên là ccc, thì các đặc điểm chính của hình thang cân bao gồm:
- Hai cạnh bên bằng nhau: AB=CDAB = CDAB=CD.
- Hai cạnh đáy song song: AD∥BCAD \parallel BCAD∥BC.
- Hai góc kề cạnh đáy bằng nhau: ∠A=∠D\angle A = \angle D∠A=∠D và ∠B=∠C\angle B = \angle C∠B=∠C.
Công thức tính diện tích hình thang cân
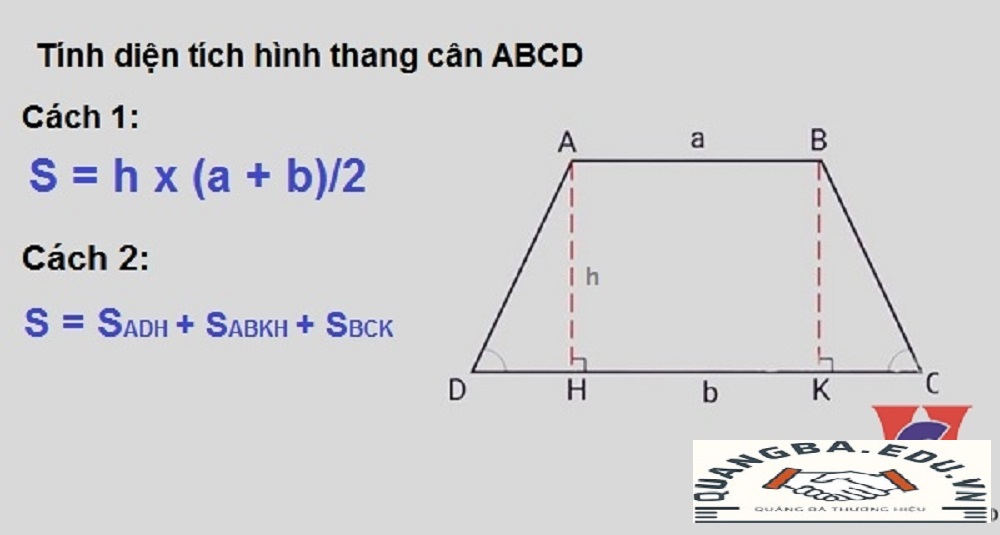
Để tính diện tích của hình thang cân, chúng ta sử dụng công thức chung để tính diện tích hình thang, đó là:
S=12×(a+b)×hS = \frac{1}{2} \times (a + b) \times hS=21×(a+b)×h
Trong đó:
- aaa và bbb là độ dài hai cạnh đáy của hình thang.
- hhh là chiều cao, được tính từ đường thẳng nối vuông góc từ một trong hai đáy lên đến đáy còn lại.
Bước tính chiều cao hhh
Trong một hình thang cân, việc tìm chiều cao hhh thường là bước quan trọng và có thể phức tạp hơn một chút so với việc tìm chiều cao trong một hình thang thông thường. Để tìm chiều cao, chúng ta có thể sử dụng định lý Pythagoras trong tam giác vuông được tạo ra bởi chiều cao, một nửa hiệu số giữa hai đáy và cạnh bên.
Giả sử, chúng ta có hình thang cân ABCDABCDABCD với ABABAB và CDCDCD là hai cạnh bên, ADADAD và BCBCBC là hai cạnh đáy với AD=aAD = aAD=a và BC=bBC = bBC=b và AB=CD=cAB = CD = cAB=CD=c.
Tính chiều cao hhh:
- Tính nửa hiệu số giữa hai cạnh đáy:
d=a−b2d = \frac{a – b}{2}d=2a−b
- Áp dụng định lý Pythagoras trong tam giác vuông để tìm chiều cao hhh:
h=c2−d2h = \sqrt{c^2 – d^2}h=c2−d2
h=c2−(a−b2)2h = \sqrt{c^2 – \left(\frac{a – b}{2}\right)^2}h=c2−(2a−b)2
Công thức đầy đủ để tính diện tích hình thang cân
Khi đã có chiều cao hhh, chúng ta có thể tính diện tích hình thang cân bằng công thức sau:
S=12×(a+b)×hS = \frac{1}{2} \times (a + b) \times hS=21×(a+b)×h
Bài viết liên quan: Số Bị Trừ Là Gì?
Thay thế hhh vào công thức:
S=12×(a+b)×c2−(a−b2)2S = \frac{1}{2} \times (a + b) \times \sqrt{c^2 – \left(\frac{a – b}{2}\right)^2}S=21×(a+b)×c2−(2a−b)2
Ví dụ minh họa
Ví dụ 1:
Cho hình thang cân ABCDABCDABCD với:
- Độ dài hai cạnh đáy AD=10AD = 10AD=10 cm và BC=6BC = 6BC=6 cm.
- Độ dài hai cạnh bên AB=CD=5AB = CD = 5AB=CD=5 cm.
Ta có:
a=10a = 10a=10 b=6b = 6b=6 c=5c = 5c=5
Tính nửa hiệu số giữa hai cạnh đáy:
d=10−62=2d = \frac{10 – 6}{2} = 2d=210−6=2
Áp dụng định lý Pythagoras để tìm chiều cao hhh:
h=52−22=25−4=21h = \sqrt{5^2 – 2^2} = \sqrt{25 – 4} = \sqrt{21}h=52−22=25−4=21
Tính diện tích hình thang cân:
S=12×(10+6)×21S = \frac{1}{2} \times (10 + 6) \times \sqrt{21}S=21×(10+6)×21 S=12×16×21S = \frac{1}{2} \times 16 \times \sqrt{21}S=21×16×21 S=8×21S = 8 \times \sqrt{21}S=8×21
Kết quả cuối cùng:
S≈36.66 cm2S \approx 36.66 \, \text{cm}^2S≈36.66cm2
Ví dụ 2:
Cho hình thang cân EFGHEFGHEFGH với:
- Độ dài hai cạnh đáy EF=12EF = 12EF=12 cm và GH=8GH = 8GH=8 cm.
- Độ dài hai cạnh bên EH=FG=7EH = FG = 7EH=FG=7 cm.
Ta có:
a=12a = 12a=12 b=8b = 8b=8 c=7c = 7c=7
Tính nửa hiệu số giữa hai cạnh đáy:
d=12−82=2d = \frac{12 – 8}{2} = 2d=212−8=2
Áp dụng định lý Pythagoras để tìm chiều cao hhh:
h=72−22=49−4=45h = \sqrt{7^2 – 2^2} = \sqrt{49 – 4} = \sqrt{45}h=72−22=49−4=45
Tính diện tích hình thang cân:
S=12×(12+8)×45S = \frac{1}{2} \times (12 + 8) \times \sqrt{45}S=21×(12+8)×45 S=12×20×45S = \frac{1}{2} \times 20 \times \sqrt{45}S=21×20×45 S=10×45S = 10 \times \sqrt{45}S=10×45
Kết quả cuối cùng:
S≈67.08 cm2S \approx 67.08 \, \text{cm}^2S≈67.08cm2
Bài viết xem thêm: Tính Chất Hình Thang Vuông
Kết luận nội dung
Việc tính diện tích hình thang cân đòi hỏi chúng ta phải hiểu rõ về các đặc điểm hình học của hình thang cân và áp dụng các công thức toán học một cách chính xác. Hy vọng rằng qua bài viết này, bạn đã nắm vững cách tính diện tích hình thang cân và có thể áp dụng vào các bài toán thực tế. Chúc bạn học tốt và thành công!