Chứng Minh Hình Thang Cân

Chứng Minh Hình Thang Cân – Hình thang cân là một khái niệm quan trọng trong hình học, được định nghĩa là một hình thang có hai cạnh bên bằng nhau và hai cạnh đáy song song. Điểm nổi bật của hình thang cân nằm ở sự đối xứng của nó, tạo nên một cấu trúc cân đối và hài hòa. Các thuộc tính này không chỉ làm cho hình thang cân trở nên đặc biệt trong các bài toán hình học, mà còn có nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày.
Giới Thiệu Về Hình Thang Cân
Một trong những ứng dụng phổ biến của hình thang cân là trong thiết kế và xây dựng. Với đặc điểm đối xứng, hình thang cân thường được sử dụng trong kiến trúc để tạo nên các công trình có tính thẩm mỹ cao và ổn định. Ví dụ, nhiều cây cầu và cấu trúc mái nhà sử dụng hình thang cân để đảm bảo sự phân bố lực đều đặn và độ bền cao.
Bài viết liên quan: Công Thức Tính Diện Tích Tứ Giác
Trong lĩnh vực giáo dục, hình thang cân cũng đóng vai trò quan trọng trong việc giảng dạy các khái niệm cơ bản về hình học. Học sinh thường được yêu cầu chứng minh các tính chất của hình thang cân, từ đó phát triển kỹ năng tư duy logic và khả năng giải quyết vấn đề. Nhờ vào tính chất đối xứng và đơn giản của nó, hình thang cân dễ dàng được nhận biết và là một trong những hình học cơ bản mà học sinh tiếp cận đầu tiên.
Không chỉ dừng lại ở đó, hình thang cân còn được ứng dụng trong nhiều lĩnh vực khác như thiết kế đồ họa, nghệ thuật trang trí, và thậm chí cả trong nghiên cứu khoa học. Các đặc điểm của hình thang cân giúp nó trở thành một biểu tượng cho sự cân đối và hoàn hảo trong nhiều ngữ cảnh khác nhau.
Định Nghĩa Và Đặc Điểm Của Hình Thang Cân
Hình thang cân là một loại hình thang đặc biệt với những đặc điểm riêng biệt giúp nó được nhận diện dễ dàng. Theo định nghĩa, hình thang cân là một hình thang có hai cạnh bên bằng nhau. Điều này có nghĩa là hai cạnh kề không song song trong hình thang cân có độ dài bằng nhau.
Thêm vào đó, hình thang cân còn có một đặc điểm quan trọng khác là hai góc kề một cạnh đáy của nó bằng nhau. Điều này có nghĩa là các góc ở hai đầu của một trong hai cạnh đáy của hình thang cân có giá trị bằng nhau. Chính đặc điểm này làm cho hình thang cân có tính chất đối xứng, giúp nó dễ dàng được nhận biết và phân biệt với các loại hình học khác.
Trong hình học, để dễ dàng hình dung và hiểu rõ hơn về hình thang cân, chúng ta thường sử dụng các hình vẽ minh họa. Ví dụ, nếu chúng ta có một hình thang ABCD với các cạnh AB và CD là hai cạnh đáy song song, thì hai cạnh bên AD và BC sẽ bằng nhau. Đồng thời, các góc tại đỉnh A và D, hoặc B và C sẽ bằng nhau.
Việc hiểu rõ các đặc điểm này không chỉ giúp chúng ta nhận diện hình thang cân một cách dễ dàng, mà còn là cơ sở quan trọng cho các bước chứng minh tiếp theo trong các bài toán hình học. Sự cân đối và tính chất đối xứng của hình thang cân là những yếu tố giúp nó có nhiều ứng dụng trong toán học cũng như trong thực tiễn.
Cách Chứng Minh Hình Thang Cân Bằng Phép Đối Xứng
Chứng minh hình thang cân bằng phương pháp đối xứng là một cách tiếp cận phổ biến và hiệu quả trong hình học. Đặc điểm chính của hình thang cân là hai cạnh bên bằng nhau và hai góc kề cạnh đáy bằng nhau. Để chứng minh điều này, chúng ta sẽ sử dụng đối xứng trục.
Trước hết, ta cần xác định trục đối xứng của hình thang. Trục đối xứng này sẽ đi qua trung điểm của hai cạnh đáy. Giả sử hình thang ABCD, trong đó AB và CD là hai cạnh đáy và AD, BC là hai cạnh bên. Ta xác định trung điểm M của cạnh đáy AB và trung điểm N của cạnh đáy CD. Khi đó, đường thẳng MN chính là trục đối xứng của hình thang ABCD.
Bây giờ, hãy xem xét hình thang ABCD đối xứng qua trục MN. Theo đặc điểm của đối xứng trục, mỗi điểm trên hình thang sẽ có một điểm đối xứng tương ứng. Cụ thể, điểm A sẽ đối xứng với điểm B, và điểm D sẽ đối xứng với điểm C. Do đó, cạnh AD sẽ đối xứng với cạnh BC.
Vì AD và BC là các đoạn thẳng đối xứng nên chúng có chiều dài bằng nhau. Điều này chứng tỏ rằng hai cạnh bên của hình thang cân bằng nhau. Tiếp theo, ta xét góc kề cạnh đáy. Do tính chất của đối xứng trục, góc tại điểm A sẽ đối xứng với góc tại điểm B, và góc tại điểm D sẽ đối xứng với góc tại điểm C. Do đó, hai góc kề cạnh đáy của hình thang cân sẽ bằng nhau.
Như vậy, thông qua phép đối xứng, chúng ta đã chứng minh được rằng trong hình thang cân, hai cạnh bên bằng nhau và hai góc kề cạnh đáy bằng nhau. Phương pháp này không chỉ giúp xác nhận đặc điểm của hình thang cân mà còn cung cấp một cách nhìn trực quan và logic về cấu trúc đối xứng của nó.
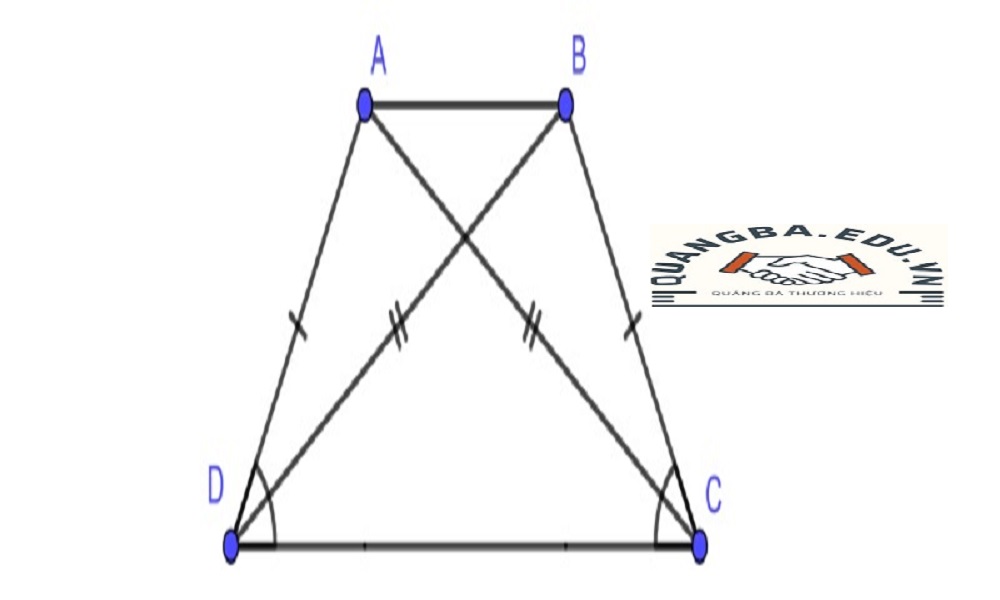
Chứng Minh Hình Thang Cân Bằng Tam Giác Đồng Dạng
Chứng minh hình thang cân có thể được thực hiện một cách hiệu quả bằng cách sử dụng các tam giác đồng dạng. Phương pháp này tận dụng các tính chất của tam giác đồng dạng để thiết lập các mối quan hệ tỷ lệ và đồng dạng, từ đó giúp chứng minh các đặc điểm của hình thang cân.
Đầu tiên, hãy xem xét một hình thang cân ABCD với đáy lớn AB và đáy nhỏ CD. Chia hình thang này thành hai tam giác bằng cách kéo dài đường cao từ đỉnh A và đỉnh B xuống đáy nhỏ CD, tạo thành hai tam giác vuông ADP và BCP (với P là giao điểm của các đường cao này với CD). Trong trường hợp này, tam giác ADP và BCP là hai tam giác vuông có chung một góc tại đỉnh P, và hai góc còn lại của chúng là các góc nhọn của hình thang cân.
Kế đến, ta có thể sử dụng các tính chất của tam giác đồng dạng để chứng minh các cạnh tương ứng của hai tam giác này tỉ lệ với nhau. Do hình thang ABCD cân, hai cạnh bên AD và BC bằng nhau. Điều này có nghĩa rằng hai tam giác ADP và BCP có các cạnh tương ứng tỷ lệ với nhau, cụ thể là AD/BC = DP/PC. Vì DP và PC là các đoạn thẳng trên cùng một đường thẳng CD, chúng bằng nhau. Do đó, tam giác ADP và BCP là đồng dạng với nhau theo tỉ lệ 1:1.
Cuối cùng, các tính chất của tam giác đồng dạng giúp ta chứng minh rằng các góc tương ứng của tam giác ADP và BCP bằng nhau, cụ thể là góc A và góc B của hình thang ABCD bằng nhau. Điều này chứng tỏ rằng các góc kề đáy của hình thang cân bằng nhau, và do đó, hình thang ABCD là hình thang cân.
Ứng Dụng Định Lý Talet Trong Chứng Minh Hình Thang Cân
Định lý Talet (hay còn gọi là định lý Thales) là một công cụ mạnh mẽ trong hình học, đặc biệt hữu ích trong việc chứng minh hình thang cân. Định lý này phát biểu rằng nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại, thì nó sẽ chia hai cạnh đó thành những đoạn tỉ lệ. Ứng dụng của định lý Talet không chỉ dừng lại ở việc chứng minh các quan hệ tỉ lệ mà còn có thể được dùng để chứng minh các tính chất hình học của hình thang cân.
Hãy xem xét một ví dụ cụ thể để minh họa. Giả sử chúng ta có hình thang ABCD với AD và BC là hai cạnh đáy và AB, CD là hai cạnh bên. Để chứng minh rằng hình thang này là hình thang cân, chúng ta cần chứng minh rằng AB = CD. Bằng cách sử dụng định lý Talet, chúng ta có thể thực hiện điều này.
Đầu tiên, kẻ đường thẳng EF song song với hai cạnh đáy AD và BC, cắt hai cạnh bên AB tại E và CD tại F. Theo định lý Talet, ta có:
AE/EB = AF/FC
Vì EF song song với AD và BC, nên các đoạn thẳng AE, EB, AF, và FC sẽ chia các cạnh AB và CD thành những đoạn tỉ lệ. Nếu ta chọn E và F sao cho AE = EB và AF = FC, điều này có nghĩa là AB = CD. Như vậy, ta đã chứng minh được rằng hình thang ABCD là hình thang cân.
Một ví dụ khác là khi chúng ta có một hình thang cân ABCD và cần xác định độ dài của các đoạn thẳng chia đôi các cạnh bên. Giả sử M và N là trung điểm của AB và CD, ta sẽ có AM = MB và CN = ND. Sử dụng định lý Talet, ta có thể suy ra rằng đoạn thẳng MN sẽ song song với hai cạnh đáy và chia hình thang thành hai hình thang nhỏ hơn có tỉ lệ các cạnh tương ứng.
Như vậy, định lý Talet không chỉ giúp chúng ta giải quyết các bài toán liên quan đến tỉ lệ mà còn cung cấp một phương pháp hiệu quả để chứng minh và xác định các tính chất của hình thang cân.
Chứng Minh Hình Thang Cân Bằng Phép Biến Hình
Để chứng minh một hình thang cân, chúng ta có thể sử dụng các phép biến hình như phép quay, phép tịnh tiến, và phép dời hình. Mỗi phương pháp này cung cấp một cách tiếp cận khác nhau để xác định và kiểm tra tính chất đối xứng của hình thang cân.
- Đầu tiên, phép quay là một công cụ mạnh mẽ để chứng minh tính chất đối xứng. Khi thực hiện phép quay một góc 180 độ quanh trung điểm của cạnh đáy lớn, chúng ta có thể nhận thấy rằng hai cạnh bên của hình thang cân sẽ trùng khớp với nhau nếu chúng có độ dài bằng nhau và song song với nhau. Điều này xác nhận rằng hai góc ở đáy lớn là bằng nhau, một trong những đặc điểm quan trọng của hình thang cân.
- Thứ hai, phép tịnh tiến cũng là một phương pháp hữu ích. Khi di chuyển một cạnh của hình thang song song với chính nó và giữ nguyên khoảng cách giữa hai cạnh đáy, chúng ta có thể thấy rằng hai cạnh bên vẫn giữ nguyên độ dài và vị trí. Điều này chứng minh rằng hai cạnh bên song song và bằng nhau, đặc điểm cốt lõi của hình thang cân.
- Cuối cùng, phép dời hình có thể được sử dụng để xác định tính chất đối xứng của hình thang cân. Bằng cách dời hình toàn bộ hình thang theo một hướng nhất định, chúng ta có thể kiểm tra xem các cạnh bên và góc có giữ nguyên tính chất đối xứng hay không. Nếu các cạnh và góc vẫn giữ nguyên các tính chất này sau khi dời hình, điều đó xác nhận tính chất đối xứng của hình thang cân.
Nhờ vào các phép biến hình như phép quay, phép tịnh tiến, và phép dời hình, chúng ta có thể dễ dàng chứng minh và xác nhận các tính chất đối xứng và các đặc điểm đặc trưng của hình thang cân. Các phương pháp này không chỉ cung cấp cách tiếp cận trực quan mà còn giúp tăng cường khả năng hiểu biết và giải thích một cách logic về hình thang cân.
Bài Tập Và Ví Dụ Minh Họa
Để hiểu rõ hơn về việc chứng minh hình thang cân, chúng ta sẽ đi qua một số bài tập và ví dụ minh họa cụ thể. Những bài tập này sẽ cung cấp lời giải chi tiết nhằm giúp người đọc thực hành và nắm vững kiến thức.
Bài Tập 1: Cho hình thang ABCD với AB // CD, và góc A = góc D. Chứng minh rằng hình thang ABCD là hình thang cân.
Giải:
– Ta có AB // CD nên góc A và góc D là hai góc trong cùng phía, do đó góc A + góc D = 180 độ.
– Vì góc A = góc D nên 2 góc A = 180 độ.
– Do đó, góc A = 90 độ và góc D = 90 độ.
– Trong tam giác vuông ABD, cạnh AB là cạnh đối diện với góc vuông, do đó AB = CD.
– Vậy, hình thang ABCD là hình thang cân.
Bài Tập 2: Cho hình thang cân ABCD với AB // CD, AC và BD cắt nhau tại điểm O. Chứng minh rằng O là trung điểm của AC và BD.
Giải:
– Vì ABCD là hình thang cân nên AB = CD và góc A = góc D, góc B = góc C.
– Xét tam giác AOB và tam giác COD:
+ Cạnh AB = CD (giả thiết)
+ Góc OAB = góc OCD (góc đối đỉnh)
+ Góc OBA = góc ODC (góc so le trong)
– Do đó, tam giác AOB đồng dạng với tam giác COD theo trường hợp góc-góc-góc.
– Từ đó suy ra, OA = OC và OB = OD, nghĩa là O là trung điểm của AC và BD.
Những bài tập và ví dụ minh họa trên giúp chúng ta thấy rõ hơn về cách chứng minh hình thang cân. Qua việc thực hành và giải quyết các bài toán này, người học có thể củng cố kiến thức và hiểu sâu hơn về khái niệm hình thang cân.
Bài viết xem thêm: Khối Lập Phương Là Gì?
Kết Luận nội dung
Trong bài viết này, chúng ta đã cùng nhau khám phá và chứng minh các phương pháp khác nhau để xác định và chứng minh hình thang cân. Việc hiểu rõ và áp dụng các phương pháp này không chỉ giúp nâng cao khả năng giải quyết bài toán hình học mà còn phát triển tư duy logic và kỹ năng phân tích của người học.