Công Thức Đạo Hàm
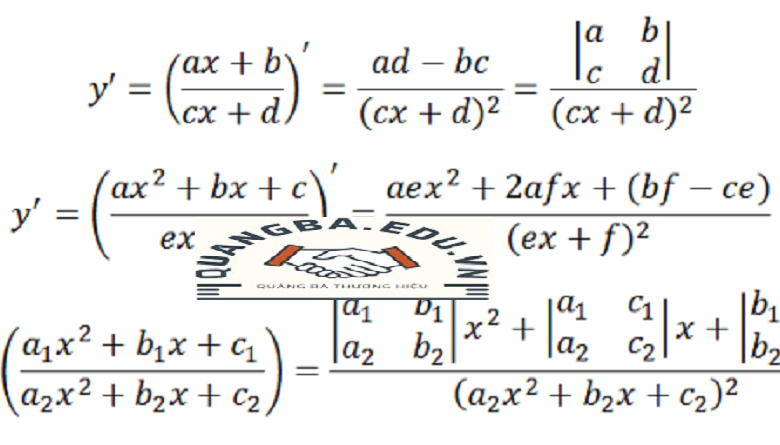
Công Thức Đạo Hàm là một khái niệm quan trọng trong toán học, đặc biệt trong lĩnh vực phân tích toán học và giải tích. Đạo hàm của một hàm số tại một điểm cho biết tốc độ thay đổi của hàm số đó tại điểm đó. Nói cách khác, đạo hàm đo lường sự thay đổi nhỏ nhất của một đại lượng này so với đại lượng khác. Định nghĩa chặt chẽ của đạo hàm là giới hạn của tỉ số sự thay đổi của giá trị hàm số và sự thay đổi của biến độc lập khi biến độc lập tiến tới giá trị cụ thể.
Giới Thiệu Về Đạo Hàm: Khám Phá Toàn Diện và Ứng Dụng Thực Tiễn
Ý nghĩa của đạo hàm trong toán học rất đa dạng. Đạo hàm giúp chúng ta hiểu rõ hơn về sự biến đổi của các hàm số, từ đó có thể áp dụng vào nhiều lĩnh vực khác nhau như vật lý, kinh tế, sinh học và kỹ thuật. Chẳng hạn, trong vật lý, đạo hàm được sử dụng để mô tả tốc độ và gia tốc của các đối tượng chuyển động. Trong kinh tế, đạo hàm giúp phân tích sự thay đổi của các chỉ số kinh tế như lợi nhuận và chi phí.
Lịch sử phát triển của đạo hàm gắn liền với sự phát triển của giải tích. Đạo hàm lần đầu tiên được phát triển bởi các nhà toán học như Isaac Newton và Gottfried Wilhelm Leibniz vào thế kỷ 17. Newton và Leibniz đã phát triển độc lập các phương pháp giải tích đạo hàm và tích phân, mặc dù phương pháp của họ có những khác biệt nhất định. Công trình của họ đã đặt nền tảng cho nhiều phát triển sau này trong toán học và khoa học.
Bài viết liên quan: Bài Tập Thì Hiện Tại Đơn
Nhiều nhà toán học nổi tiếng đã đóng góp quan trọng vào sự phát triển của lý thuyết đạo hàm, bao gồm Joseph-Louis Lagrange, Augustin-Louis Cauchy và Karl Weierstrass. Những đóng góp của họ không chỉ giúp củng cố các khái niệm cơ bản mà còn mở rộng phạm vi ứng dụng của đạo hàm trong nhiều lĩnh vực khác nhau.
Định Nghĩa Đạo Hàm và Ký Hiệu
Trong toán học, đạo hàm là một khái niệm cơ bản trong giải tích, dùng để đo lường sự thay đổi của một hàm số theo một biến số. Đạo hàm của một hàm số tại một điểm cụ thể được xác định là giới hạn của tỷ số giữa sự thay đổi của hàm số và sự thay đổi của biến số khi biến số tiến đến điểm đó. Cụ thể, nếu chúng ta có một hàm số y = f(x), đạo hàm của hàm số này tại điểm x = a được ký hiệu là f'(a) và được định nghĩa như sau:
f'(a) = lim h→0 (f(a+h) – f(a)) / h
Để biểu diễn đạo hàm, có một số ký hiệu phổ biến được sử dụng trong toán học. Ký hiệu d/dx (đọc là “d trên dx”) biểu thị đạo hàm của một hàm số y theo biến số x. Ví dụ, nếu y = f(x), thì đạo hàm của y theo x sẽ được viết là dy/dx hoặc d(f(x))/dx. Một ký hiệu khác là f'(x), trong đó dấu phẩy đứng phía trên hàm số biểu thị đạo hàm của hàm số đó. Ngoài ra, ký hiệu Df(x) cũng thường được sử dụng để biểu diễn đạo hàm của hàm số f(x).
Việc tính đạo hàm tại một điểm cụ thể không chỉ quan trọng trong lý thuyết mà còn có nhiều ứng dụng thực tiễn. Để tính đạo hàm của một hàm số tại một điểm cụ thể, chúng ta sử dụng công thức đạo hàm và thay thế giá trị của biến số vào công thức đó. Ví dụ, nếu f(x) = x², thì đạo hàm của f(x) là f'(x) = 2x. Do đó, đạo hàm của hàm số này tại điểm x = 3 là f'(3) = 2*3 = 6.
Như vậy, việc hiểu và sử dụng đúng các ký hiệu đạo hàm là rất quan trọng trong việc giải quyết các bài toán liên quan đến sự thay đổi của các hàm số. Các ký hiệu này không chỉ giúp biểu diễn các đạo hàm một cách rõ ràng mà còn giúp chúng ta dễ dàng tính toán và áp dụng chúng trong các bài toán cụ thể.
Các Công Thức Đạo Hàm Cơ Bản
Trong lĩnh vực toán học, việc nắm vững các công thức đạo hàm cơ bản là vô cùng quan trọng. Các công thức này không chỉ là nền tảng cho các khái niệm phức tạp hơn mà còn có ứng dụng thực tiễn rộng rãi. Dưới đây là danh sách các công thức đạo hàm cơ bản mà mọi người học toán đều cần biết.
1. Đạo hàm của hàm số hằng
Đối với một hàm số hằng, không thay đổi theo biến số, đạo hàm của nó luôn bằng 0. Công thức này được biểu diễn như sau:
Nếu \( f(x) = c \), thì \( f'(x) = 0 \).
Ví dụ: \( f(x) = 5 \), thì \( f'(x) = 0 \).
2. Đạo hàm của hàm số bậc nhất
Hàm số bậc nhất có dạng \( f(x) = ax + b \). Đạo hàm của nó là một hằng số và bằng hệ số của \( x \):
Nếu \( f(x) = ax + b \), thì \( f'(x) = a \).
Ví dụ: \( f(x) = 3x + 2 \), thì \( f'(x) = 3 \).
3. Đạo hàm của hàm số bậc hai
Hàm số bậc hai có dạng \( f(x) = ax^2 + bx + c \). Đạo hàm của nó là một hàm số bậc nhất:
Nếu \( f(x) = ax^2 + bx + c \), thì \( f'(x) = 2ax + b \).
Ví dụ: \( f(x) = 2x^2 + 3x + 1 \), thì \( f'(x) = 4x + 3 \).
4. Đạo hàm của hàm số mũ
Hàm số mũ có dạng \( f(x) = e^x \) hoặc \( f(x) = a^x \) (với \( a \) là một hằng số). Đạo hàm của nó được xác định như sau:
Nếu \( f(x) = e^x \), thì \( f'(x) = e^x \).
Nếu \( f(x) = a^x \), thì \( f'(x) = a^x \ln(a) \).
Ví dụ: \( f(x) = e^x \), thì \( f'(x) = e^x \).
Ví dụ: \( f(x) = 2^x \), thì \( f'(x) = 2^x \ln(2) \).
Các công thức đạo hàm cơ bản này không chỉ là nền tảng quan trọng trong việc học toán mà còn giúp giải quyết nhiều vấn đề thực tiễn trong các lĩnh vực khác nhau như vật lý, kinh tế, và kỹ thuật. Sự hiểu biết sâu sắc về chúng sẽ tạo điều kiện thuận lợi cho việc áp dụng các phương pháp toán học vào thực tế.
Quy Tắc Đạo Hàm
Để tính đạo hàm của các hàm số phức tạp hơn, chúng ta cần áp dụng một số quy tắc quan trọng. Đầu tiên là quy tắc tổng, giúp chúng ta tính đạo hàm của tổng hai hay nhiều hàm số. Quy tắc này nói rằng đạo hàm của tổng hai hàm số là tổng của các đạo hàm của từng hàm số đó. Cụ thể, nếu \( f(x) \) và \( g(x) \) là hai hàm số, thì đạo hàm của \( f(x) + g(x) \) sẽ là \( f'(x) + g'(x) \).
Tiếp theo, quy tắc tích cho phép chúng ta tính đạo hàm của tích hai hàm số. Quy tắc này phát biểu rằng nếu \( u(x) \) và \( v(x) \) là hai hàm số, thì đạo hàm của tích \( u(x) \cdot v(x) \) sẽ là \( u'(x) \cdot v(x) + u(x) \cdot v'(x) \). Ví dụ, nếu \( u(x) = x^2 \) và \( v(x) = e^x \), thì đạo hàm của \( x^2 \cdot e^x \) là \( 2x \cdot e^x + x^2 \cdot e^x \).
Quy tắc thương giúp chúng ta tính đạo hàm của thương hai hàm số. Nếu \( u(x) \) và \( v(x) \) là hai hàm số, thì đạo hàm của thương \( \frac{u(x)}{v(x)} \) sẽ là \( \frac{u'(x) \cdot v(x) – u(x) \cdot v'(x)}{v(x)^2} \). Ví dụ, với \( u(x) = x^2 \) và \( v(x) = \sin(x) \), đạo hàm của \( \frac{x^2}{\sin(x)} \) là \( \frac{2x \cdot \sin(x) – x^2 \cdot \cos(x)}{\sin(x)^2} \).
Cuối cùng, quy tắc chuỗi là công cụ mạnh mẽ để tính đạo hàm của các hàm hợp. Nếu \( y = g(f(x)) \), thì đạo hàm của \( y \) là \( g'(f(x)) \cdot f'(x) \). Ví dụ, nếu \( y = \sin(x^2) \), thì đạo hàm của \( y \) là \( \cos(x^2) \cdot 2x \).
Những quy tắc trên là cơ sở để chúng ta có thể tính toán đạo hàm của các hàm số phức tạp một cách hiệu quả và chính xác. Mỗi quy tắc đều có ứng dụng quan trọng trong toán học và các lĩnh vực liên quan, giúp chúng ta giải quyết các bài toán thực tiễn một cách dễ dàng hơn.
Đạo Hàm Của Các Hàm Số Đặc Biệt
Trong toán học, việc tính đạo hàm của các hàm số đặc biệt như hàm số lượng giác, hàm số logarit, và hàm số mũ là rất quan trọng. Đạo hàm của các hàm số này không chỉ có ý nghĩa lý thuyết mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực khoa học, kỹ thuật và kinh tế.
- Hàm Số Lượng Giác
Hàm số lượng giác bao gồm các hàm như sin(x), cos(x), và tan(x). Công thức đạo hàm của các hàm này như sau:
- Đạo hàm của sin(x) là cos(x): (d/dx) sin(x) = cos(x)
- Đạo hàm của cos(x) là -sin(x): (d/dx) cos(x) = -sin(x)
- Đạo hàm của tan(x) là sec²(x): (d/dx) tan(x) = sec²(x)
Ví dụ minh họa: Tính đạo hàm của hàm số f(x) = sin(x) + cos(x). Sử dụng các công thức trên, ta có: f'(x) = cos(x) – sin(x).
- Hàm Số Logarit
Hàm logarit là một trong những hàm số quan trọng trong toán học, đặc biệt là hàm logarit tự nhiên ln(x). Công thức đạo hàm của hàm logarit tự nhiên là:
Đạo hàm của ln(x) là 1/x: (d/dx) ln(x) = 1/x
Ví dụ minh họa: Tính đạo hàm của hàm số g(x) = ln(x²). Sử dụng quy tắc chuỗi, ta có: g'(x) = (1/x²) * 2x = 2/x.
- Hàm Số Mũ
Hàm số mũ bao gồm các hàm như e^x và a^x (với a là một hằng số dương). Công thức đạo hàm của các hàm này như sau:
- Đạo hàm của e^x là chính nó: (d/dx) e^x = e^x
- Đạo hàm của a^x là a^x * ln(a): (d/dx) a^x = a^x * ln(a)
Ví dụ minh họa: Tính đạo hàm của hàm số h(x) = 3^x. Sử dụng công thức trên, ta có: h'(x) = 3^x * ln(3).
Việc nắm vững cách tính đạo hàm của các hàm số đặc biệt này sẽ giúp ích rất nhiều trong việc giải quyết các bài toán phức tạp hơn và ứng dụng vào các lĩnh vực khác nhau.
Ứng Dụng Của Đạo Hàm Trong Thực Tiễn
Đạo hàm, một khái niệm cơ bản trong toán học, không chỉ tồn tại trong lý thuyết mà còn có vô vàn ứng dụng thực tiễn trong nhiều lĩnh vực khác nhau. Một trong những ứng dụng phổ biến nhất của đạo hàm là trong vật lý. Đạo hàm giúp xác định tốc độ và gia tốc của một vật thể chuyển động. Ví dụ, khi chúng ta biết vị trí của một vật thể theo thời gian, đạo hàm của hàm vị trí sẽ cho ta biết tốc độ thay đổi vị trí, trong khi đó, đạo hàm bậc hai sẽ cho biết gia tốc của vật thể.
Trong kinh tế, đạo hàm được sử dụng để phân tích và tối ưu hóa. Một ứng dụng cụ thể là trong việc tìm hiểu lợi nhuận biên, tức là sự thay đổi của lợi nhuận khi thay đổi một đơn vị sản phẩm. Bằng cách lấy đạo hàm của hàm lợi nhuận theo số lượng sản phẩm, doanh nghiệp có thể xác định được điểm tối ưu để tối đa hóa lợi nhuận. Ngoài ra, đạo hàm cũng được dùng để phân tích độ co giãn của cầu, giúp doanh nghiệp điều chỉnh giá bán sao cho hợp lý.
Trong kỹ thuật, đặc biệt là trong lĩnh vực điều khiển tự động, đạo hàm đóng vai trò quan trọng trong việc thiết kế các hệ thống điều khiển. Các hệ thống này thường sử dụng đạo hàm để dự đoán và điều chỉnh phản hồi của hệ thống theo thời gian thực. Ví dụ, trong các bộ điều khiển PID (Proportional-Integral-Derivative), thành phần đạo hàm giúp điều chỉnh tốc độ thay đổi của tín hiệu điều khiển, đảm bảo hệ thống hoạt động ổn định và hiệu quả.
Như vậy, từ việc tính toán tốc độ trong vật lý, tối ưu hóa lợi nhuận trong kinh tế, đến điều khiển hệ thống trong kỹ thuật, đạo hàm là công cụ không thể thiếu để giải quyết các vấn đề thực tiễn một cách hiệu quả. Ứng dụng của đạo hàm không chỉ giới hạn trong các lĩnh vực trên mà còn mở rộng ra nhiều lĩnh vực khác, chứng minh vai trò quan trọng của nó trong khoa học và công nghệ.

Bài Tập Thực Hành Và Giải Thích Chi Tiết
Trong quá trình học tập và nghiên cứu về đạo hàm, việc thực hành là một phần không thể thiếu. Để giúp bạn đọc nắm vững hơn về cách tính đạo hàm và áp dụng các công thức đã học, chúng tôi sẽ cung cấp một loạt các bài tập thực hành từ cơ bản đến nâng cao. Mỗi bài tập sẽ đi kèm với lời giải chi tiết và giải thích từng bước.
Bài tập 1: Tính đạo hàm của hàm số f(x) = 3x^2 + 5x – 7.
Lời giải:
Bước 1: Xác định các thành phần của hàm số. Chúng ta có hàm số f(x) = 3x^2 + 5x – 7.
Bước 2: Áp dụng các quy tắc đạo hàm cơ bản. Đạo hàm của 3x^2 là 6x, đạo hàm của 5x là 5, và đạo hàm của hằng số -7 là 0.
Bước 3: Kết hợp các kết quả lại. Ta có f'(x) = 6x + 5.
Bài tập 2: Tìm đạo hàm của hàm số g(x) = e^x * sin(x).
Lời giải:
Bước 1: Xác định các thành phần của hàm số. Chúng ta có hàm số g(x) = e^x * sin(x).
Bước 2: Áp dụng quy tắc đạo hàm của tích. Đó là (u * v)’ = u’ * v + u * v’, với u = e^x và v = sin(x).
Bước 3: Tính đạo hàm của u và v. Đạo hàm của e^x là e^x, và đạo hàm của sin(x) là cos(x).
Bước 4: Áp dụng quy tắc đạo hàm của tích. Ta có g'(x) = e^x * cos(x) + e^x * sin(x).
Bài tập 3: Tính đạo hàm bậc hai của hàm số h(x) = ln(x^2 + 1).
Lời giải:
Bước 1: Tính đạo hàm bậc nhất của hàm số. Đạo hàm của h(x) = ln(x^2 + 1) là h'(x) = (2x) / (x^2 + 1).
Bước 2: Tính đạo hàm bậc hai của hàm số. Đạo hàm của h'(x) = (2x) / (x^2 + 1) là h”(x) = (2 * (x^2 + 1) – 2x * 2x) / (x^2 + 1)^2 = (2 – 2x^2) / (x^2 + 1)^2.
Hy vọng rằng các bài tập và lời giải trên sẽ giúp bạn đọc hiểu rõ hơn về cách tính đạo hàm và áp dụng các công thức đã học vào thực tiễn. Việc luyện tập thường xuyên sẽ giúp củng cố kiến thức và nâng cao kỹ năng giải toán của bạn.
Kết Luận và Tài Liệu Tham Khảo
Trong bài viết này, chúng ta đã khám phá toàn diện về công thức đạo hàm, từ định nghĩa cơ bản đến các quy tắc phức tạp hơn như quy tắc chuỗi, quy tắc tích và quy tắc chia. Các ứng dụng thực tiễn của đạo hàm trong nhiều lĩnh vực như vật lý, kinh tế và kỹ thuật cũng đã được trình bày chi tiết, cho thấy sự quan trọng và tính ứng dụng rộng rãi của khái niệm này.
Bài viết xem thêm: Thương là phép tính gì?
Để giúp người đọc có thể tiếp tục nghiên cứu và nắm vững thêm kiến thức về đạo hàm, dưới đây là một số tài liệu tham khảo và sách học bổ ích:
Tài Liệu Tham Khảo
- “Calculus: Early Transcendentals” của James Stewart: Đây là một cuốn sách giáo trình toàn diện về giải tích, bao gồm nhiều bài tập và ví dụ về đạo hàm.
- “Advanced Engineering Mathematics” của Erwin Kreyszig: Cuốn sách này cung cấp các ứng dụng của đạo hàm trong kỹ thuật và vật lý, rất hữu ích cho sinh viên và các chuyên gia trong lĩnh vực này.
- “Principles of Mathematical Analysis” của Walter Rudin: Đây là một tài liệu học tập chuyên sâu về giải tích toán học, thích hợp cho những ai muốn hiểu sâu hơn về các khái niệm cơ bản và tiên tiến của đạo hàm.
- Các tài liệu trực tuyến: Các trang web như Khan Academy, Coursera, và MIT OpenCourseWare cung cấp nhiều khóa học và bài giảng miễn phí về giải tích và đạo hàm, giúp người học tự do tiếp cận và học hỏi theo tốc độ của riêng mình.
Hy vọng rằng những tài liệu trên sẽ giúp bạn tiếp tục khám phá và nắm vững kiến thức về đạo hàm, từ đó áp dụng hiệu quả vào các bài toán thực tiễn và nghiên cứu chuyên sâu hơn.