Đường Kính Hình Tròn
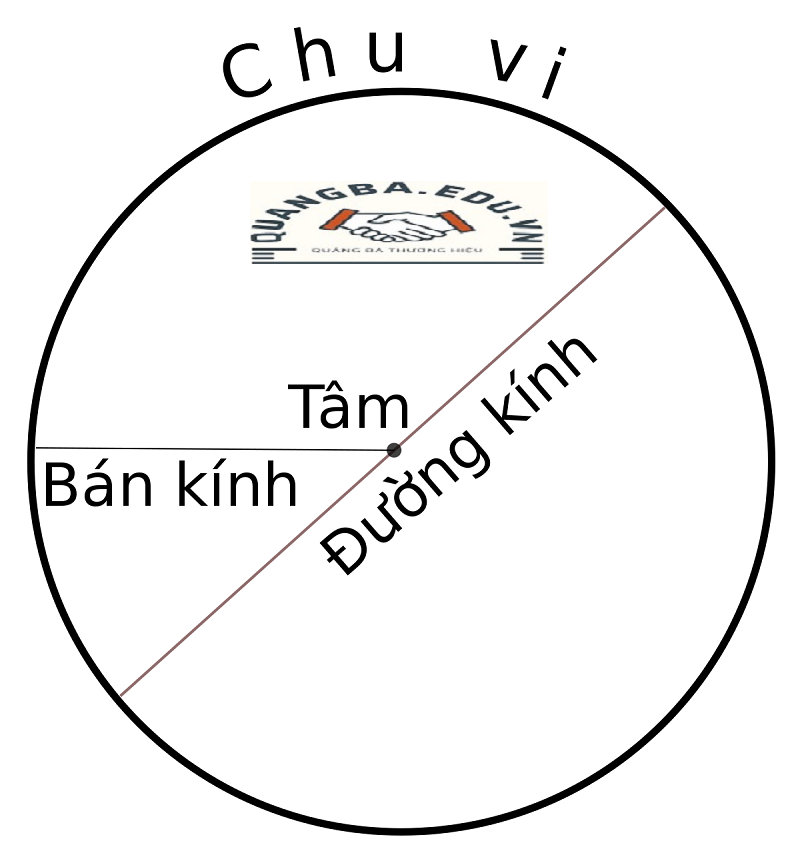
Đường kính hình tròn là một khái niệm cơ bản và quan trọng trong hình học. Đường kính được định nghĩa là đoạn thẳng đi qua tâm của hình tròn và nối hai điểm trên đường tròn đó. Đường kính có độ dài bằng hai lần bán kính, tức là đường kính = 2 * bán kính. Điều này có nghĩa rằng nếu biết bán kính của một hình tròn, chúng ta có thể dễ dàng tính toán được đường kính của nó và ngược lại.
Giới thiệu về đường kính hình tròn
Đường kính không chỉ liên quan mật thiết đến bán kính mà còn ảnh hưởng đến các yếu tố khác của hình tròn như chu vi và diện tích. Công thức tính chu vi của hình tròn là C = π * đường kính, trong đó π (pi) là hằng số toán học xấp xỉ bằng 3.14159. Tương tự, diện tích của hình tròn được tính bằng công thức A = π * (bán kính)^2, từ đó có thể suy ra rằng diện tích cũng phụ thuộc vào đường kính.
Bài viết liên quan: Rút gọn phân số
Lịch sử của khái niệm đường kính có từ rất lâu đời, từ thời kỳ cổ đại khi các nhà toán học Hy Lạp như Euclid đã nghiên cứu và phát triển các định lý liên quan đến hình tròn. Đường kính không chỉ là một yếu tố quan trọng trong hình học, mà còn có vai trò lớn trong các lĩnh vực khác như vật lý, kỹ thuật và khoa học máy tính. Ví dụ, trong kỹ thuật cơ khí, đường kính là một thông số quan trọng để thiết kế các chi tiết máy móc, từ bánh xe đến các trục quay.
Việc hiểu và tính toán đường kính hình tròn không chỉ giúp ích trong việc giải quyết các bài toán hình học mà còn có ứng dụng thực tiễn rộng rãi trong đời sống và các ngành khoa học kỹ thuật. Điều này chứng tỏ tầm quan trọng của khái niệm đường kính hình tròn trong cả lý thuyết và thực hành.
Cách tính đường kính hình tròn
Đường kính của một hình tròn là đoạn thẳng dài nhất đi qua tâm và nối hai điểm trên đường tròn. Có nhiều phương pháp để tính toán đường kính của một hình tròn, tùy thuộc vào các thông tin có sẵn như bán kính, chu vi, hoặc diện tích của hình tròn.
Trước hết, công thức cơ bản nhất để tính đường kính khi biết bán kính (r) là:
D = 2r
Nghĩa là, đường kính bằng hai lần bán kính. Ví dụ, nếu bán kính của một hình tròn là 5 cm, thì đường kính của nó sẽ là:
D = 2 x 5 = 10 cm
Tiếp theo, nếu chúng ta biết chu vi (C) của hình tròn, chúng ta có thể tính đường kính bằng công thức:
D = C / π
Ví dụ, nếu chu vi của một hình tròn là 31.4 cm, ta có thể tính đường kính như sau:
D = 31.4 / 3.14 ≈ 10 cm
Cuối cùng, khi biết diện tích (A) của một hình tròn, đường kính có thể được tính bằng công thức sau:
D = 2√(A / π)
Ví dụ, nếu diện tích của một hình tròn là 78.5 cm², chúng ta tính đường kính như sau:
D = 2√(78.5 / 3.14) ≈ 10 cm
Như vậy, thông qua các ví dụ cụ thể, chúng ta có thể thấy rằng việc tính toán đường kính của một hình tròn là một quá trình đơn giản khi ta biết đúng công thức và thông tin cần thiết. Các phương pháp này rất hữu ích trong nhiều ứng dụng thực tế, từ thiết kế kỹ thuật đến các lĩnh vực khoa học và giáo dục.
Mối quan hệ giữa đường kính và các yếu tố khác của hình tròn
Đường kính của hình tròn không chỉ là một yếu tố độc lập mà còn có mối quan hệ chặt chẽ với các yếu tố khác như bán kính, chu vi và diện tích. Hiểu rõ những mối quan hệ này sẽ giúp chúng ta dễ dàng hơn trong việc tính toán và ứng dụng các đặc tính của hình tròn trong thực tế.
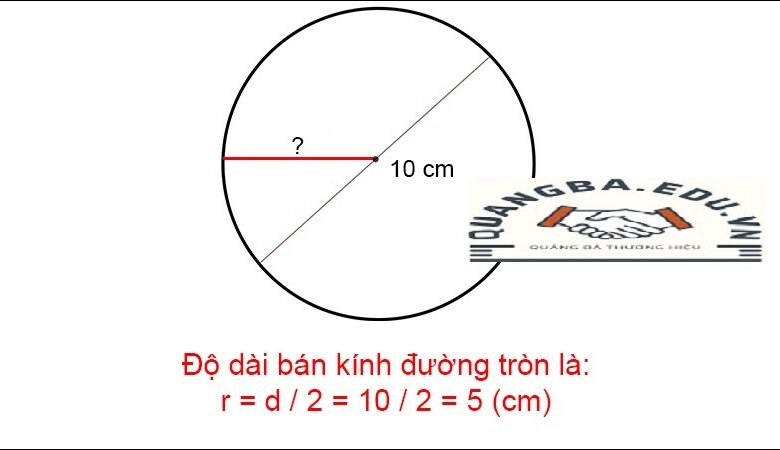
Đầu tiên, đường kính (d) của hình tròn có mối quan hệ trực tiếp với bán kính (r). Công thức đơn giản để chuyển đổi giữa hai yếu tố này là:
d = 2r
Nghĩa là, đường kính bằng hai lần bán kính. Ngược lại, bán kính cũng có thể được tính từ đường kính qua công thức:
r = d / 2
Tiếp theo, chúng ta sẽ xem xét mối quan hệ giữa đường kính và chu vi (C) của hình tròn. Chu vi của hình tròn được xác định bởi công thức:
C = πd
Đây là một công thức quan trọng cho thấy chu vi của hình tròn tỉ lệ thuận với đường kính. Khi đường kính tăng, chu vi cũng tăng theo, và ngược lại.
Cuối cùng, diện tích (A) của hình tròn cũng phụ thuộc vào đường kính. Công thức tính diện tích dựa trên đường kính là:
A = π(d/2)^2
Hoặc có thể viết lại là:
A = (πd^2) / 4
Qua công thức này, ta thấy rằng diện tích của hình tròn tỉ lệ thuận với bình phương của đường kính. Điều này có nghĩa là một sự thay đổi nhỏ ở đường kính sẽ dẫn đến một sự thay đổi lớn hơn ở diện tích.
Như vậy, việc hiểu rõ mối quan hệ giữa đường kính và các yếu tố khác của hình tròn không chỉ giúp chúng ta thực hiện các phép tính chính xác mà còn cung cấp nền tảng cho nhiều ứng dụng trong thực tế, từ thiết kế kiến trúc đến khoa học và kỹ thuật.
Ứng dụng của đường kính trong đời sống và kỹ thuật
Đường kính hình tròn không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế, đóng vai trò quan trọng trong nhiều lĩnh vực của đời sống và kỹ thuật. Một trong những lĩnh vực tiêu biểu sử dụng đường kính là ngành xây dựng. Khi thiết kế và xây dựng các công trình, từ nhà cửa đến cầu đường, việc xác định đường kính của các cấu trúc tròn như cột trụ, ống dẫn nước, và ống khói là vô cùng quan trọng. Đường kính giúp xác định khả năng chịu lực, độ bền và khả năng dẫn nước hoặc khí của các cấu trúc này.
Trong ngành cơ khí, đường kính hình tròn cũng đóng vai trò then chốt. Các bộ phận máy móc như bánh răng, trục quay, và ổ bi đều yêu cầu tính toán chính xác đường kính để đảm bảo hoạt động hiệu quả và an toàn. Ví dụ, đường kính của bánh răng ảnh hưởng trực tiếp đến tốc độ và lực truyền động của máy móc. Tương tự, đường kính của trục quay quyết định khả năng chịu tải và tốc độ quay của các bộ phận cơ khí.
Ngành y học cũng không thể thiếu sự hiện diện của đường kính. Trong việc thiết kế và sản xuất các thiết bị y tế như ống nội soi, ống thông, và kim tiêm, đường kính là một yếu tố quan trọng để đảm bảo tính chính xác và an toàn khi sử dụng. Đặc biệt, trong phẫu thuật nội soi, việc chọn đường kính phù hợp của các dụng cụ giúp giảm thiểu xâm lấn và tăng cường hiệu quả điều trị.
Cuối cùng, trong lĩnh vực nghệ thuật và thiết kế, đường kính cũng có vai trò không nhỏ. Từ thiết kế đồ họa, làm việc với các hình vẽ tròn, đến sản xuất các tác phẩm nghệ thuật điêu khắc, việc xác định đường kính chính xác giúp tạo ra các sản phẩm có tính thẩm mỹ cao và đúng theo ý đồ của người sáng tạo.
Các bài toán liên quan đến đường kính hình tròn
Trong toán học, đường kính hình tròn là một khái niệm cơ bản nhưng cũng rất đa dạng và phong phú trong ứng dụng. Các bài toán liên quan đến đường kính hình tròn không chỉ giúp học sinh hiểu sâu hơn về hình học, mà còn phát triển tư duy logic và kỹ năng giải quyết vấn đề. Dưới đây là một số bài toán thường gặp, được phân loại theo độ khó, cùng với hướng dẫn chi tiết để bạn có thể tự giải.
Bài toán cơ bản: Một bài toán đơn giản về đường kính hình tròn là yêu cầu tính đường kính khi biết bán kính. Công thức tính đường kính là d = 2r, trong đó d là đường kính và r là bán kính. Ví dụ, nếu bán kính của một hình tròn là 5 cm, thì đường kính sẽ là 10 cm.
Bài toán trung bình: Một bài toán phổ biến khác là tính chu vi của hình tròn khi biết đường kính. Công thức tính chu vi là C = πd, với π (pi) xấp xỉ bằng 3.14159. Ví dụ, nếu đường kính của một hình tròn là 8 cm, thì chu vi sẽ là khoảng 25.13 cm.
Bài toán nâng cao: Một bài toán khó hơn yêu cầu xác định diện tích của hình tròn khi biết đường kính. Công thức tính diện tích là A = πr². Trước tiên, cần tính bán kính từ đường kính bằng cách chia đôi đường kính (r = d/2), sau đó áp dụng vào công thức tính diện tích. Ví dụ, nếu đường kính là 10 cm, bán kính sẽ là 5 cm và diện tích sẽ là khoảng 78.54 cm².
Qua các bài toán trên, người đọc có thể thấy rõ tầm quan trọng của việc hiểu và áp dụng đúng các công thức liên quan đến đường kính hình tròn. Những bài toán này không chỉ giúp củng cố kiến thức mà còn là nền tảng để giải quyết các vấn đề phức tạp hơn trong toán học và thực tiễn.
Các công cụ và phần mềm hỗ trợ tính toán đường kính
Ngày nay, việc tính toán đường kính hình tròn đã trở nên dễ dàng hơn nhờ sự hỗ trợ của nhiều công cụ và phần mềm hiện đại. Các công cụ này không chỉ đơn giản hóa quá trình tính toán mà còn tăng độ chính xác và hiệu quả trong công việc. Bài viết này sẽ giới thiệu một số công cụ phổ biến, từ các ứng dụng di động đến phần mềm chuyên nghiệp, cùng với cách sử dụng chúng để tính toán đường kính một cách chính xác.
Đầu tiên, các ứng dụng di động như Calculator++, GeoGebra, và Circle Calculator là những lựa chọn phổ biến cho người dùng cá nhân. Calculator++ cung cấp các chức năng tính toán cơ bản và nâng cao, trong khi GeoGebra là một công cụ mạnh mẽ cho việc học và giảng dạy toán học với khả năng mô phỏng hình học. Circle Calculator là một ứng dụng chuyên biệt, giúp bạn tính toán nhanh chóng đường kính, bán kính, chu vi và diện tích của hình tròn chỉ với vài thao tác đơn giản.
Đối với các chuyên gia và doanh nghiệp, phần mềm chuyên nghiệp như AutoCAD, SolidWorks và MATLAB là những công cụ không thể thiếu. AutoCAD và SolidWorks là hai phần mềm thiết kế đồ họa 3D và 2D phổ biến, cho phép người dùng tạo ra các bản vẽ kỹ thuật với độ chính xác cao. Bằng cách sử dụng các lệnh và công cụ có sẵn, người dùng có thể dễ dàng tính toán đường kính và các thông số khác của hình tròn. MATLAB, một môi trường tính toán kỹ thuật mạnh mẽ, cung cấp các hàm và công cụ hỗ trợ việc tính toán và mô phỏng các yếu tố hình học, bao gồm cả đường kính hình tròn.
Cuối cùng, các công cụ trực tuyến miễn phí như Wolfram Alpha và Desmos cũng là những lựa chọn hữu ích. Wolfram Alpha cho phép người dùng nhập các biểu thức toán học và nhận kết quả tức thì, trong khi Desmos là một công cụ đồ thị trực tuyến mạnh mẽ, hỗ trợ việc vẽ và tính toán các thông số của hình tròn một cách trực quan.
Bài viết xem thêm: Bảng nhân chia
Nhờ sự phát triển của các công cụ và phần mềm này, việc tính toán đường kính hình tròn đã trở nên đơn giản và chính xác hơn bao giờ hết, đáp ứng nhu cầu từ học tập, nghiên cứu đến các ứng dụng thực tiễn trong công việc và đời sống hàng ngày.