Hình Tam Giác
Hình tam giác là một trong những hình học cơ bản và quan trọng nhất trong toán học. Nó không chỉ xuất hiện trong các bài toán cơ bản mà còn được ứng dụng rộng rãi trong kiến trúc, kỹ thuật và nghệ thuật. Bài viết này sẽ giới thiệu chi tiết về hình tam giác, từ định nghĩa, phân loại, tính chất đến các ứng dụng thực tế.
Định Nghĩa và Cấu Trúc Của Hình Tam Giác
Hình tam giác là một hình hình học phẳng được tạo bởi ba đoạn thẳng nối ba điểm không thẳng hàng. Ba điểm này gọi là ba đỉnh của tam giác, và ba đoạn thẳng là ba cạnh của tam giác. Tổng các góc trong của một tam giác luôn bằng 180 độ.
Phân Loại Hình Tam Giác
Hình tam giác có thể được phân loại dựa trên độ dài các cạnh hoặc số đo các góc.
Bài viết liên quan: 1ha bằng bao nhiêu m2
- Phân loại theo độ dài các cạnh:
- Tam giác đều: Tam giác có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc bằng 60 độ.
- Tam giác cân: Tam giác có hai cạnh bằng nhau và hai góc ở đáy bằng nhau.
- Tam giác thường: Tam giác có ba cạnh không bằng nhau và ba góc cũng không bằng nhau.
- Phân loại theo số đo các góc:
- Tam giác vuông: Tam giác có một góc bằng 90 độ.
- Tam giác nhọn: Tam giác có ba góc đều nhỏ hơn 90 độ.
- Tam giác tù: Tam giác có một góc lớn hơn 90 độ.
Tính Chất Cơ Bản của Hình Tam Giác
- Tổng các góc trong của tam giác: Tổng ba góc trong của bất kỳ tam giác nào cũng bằng 180 độ.
- Định lý Pythagore: Trong một tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông.
c2=a2+b2c^2 = a^2 + b^2c2=a2+b2
Trong đó ccc là độ dài cạnh huyền, aaa và bbb là độ dài hai cạnh góc vuông.
- Bất đẳng thức tam giác: Tổng độ dài hai cạnh bất kỳ của một tam giác luôn lớn hơn độ dài cạnh còn lại.
a+b>ca + b > ca+b>c a+c>ba + c > ba+c>b b+c>ab + c > ab+c>a
- Định lý sin và định lý cos:
- Định lý sin: Tỷ số giữa độ dài một cạnh và sin của góc đối diện với cạnh đó là như nhau đối với cả ba cạnh của tam giác.
asinA=bsinB=csinC\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}sinAa=sinBb=sinCc
- Định lý cos: Bình phương độ dài của một cạnh bằng tổng bình phương độ dài hai cạnh còn lại trừ đi hai lần tích của chúng nhân với cos của góc giữa hai cạnh đó.
c2=a2+b2−2abcosCc^2 = a^2 + b^2 – 2ab \cos Cc2=a2+b2−2abcosC
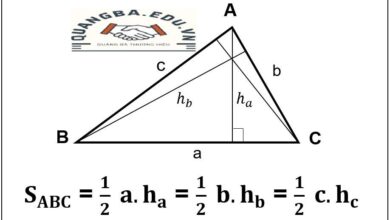
Các Công Thức Tính Diện Tích Tam Giác
Diện tích của một tam giác có thể được tính bằng nhiều công thức khác nhau tùy thuộc vào thông tin có sẵn.
- Công thức cơ bản:
S=12×đaˊy×chieˆˋu caoS = \frac{1}{2} \times \text{đáy} \times \text{chiều cao}S=21×đaˊy×chieˆˋu cao
- Công thức Heron: Áp dụng khi biết độ dài ba cạnh của tam giác.
S=s(s−a)(s−b)(s−c)S = \sqrt{s(s-a)(s-b)(s-c)}S=s(s−a)(s−b)(s−c)
Trong đó sss là nửa chu vi của tam giác:
s=a+b+c2s = \frac{a + b + c}{2}s=2a+b+c
- Diện tích tam giác vuông:
S=12×a×bS = \frac{1}{2} \times a \times bS=21×a×b
Trong đó aaa và bbb là hai cạnh góc vuông.
- Diện tích tam giác đều:
S=34×a2S = \frac{\sqrt{3}}{4} \times a^2S=43×a2
Trong đó aaa là độ dài cạnh của tam giác đều.
Ứng Dụng Thực Tế của Hình Tam Giác
Hình tam giác không chỉ là một khái niệm toán học mà còn có rất nhiều ứng dụng thực tế.
- Kiến trúc và xây dựng:
Trong kiến trúc và xây dựng, hình tam giác thường được sử dụng để tạo ra các cấu trúc ổn định và bền vững. Ví dụ, các dầm và giàn mái thường có dạng tam giác để phân bố lực đều và tăng cường độ bền.
- Kỹ thuật và cơ học:
Trong kỹ thuật, hình tam giác được sử dụng trong thiết kế các khung xe, cầu và các cấu trúc khác để đảm bảo tính ổn định và khả năng chịu lực tốt.
- Nghệ thuật và thiết kế:
Trong nghệ thuật và thiết kế, hình tam giác thường được sử dụng để tạo ra các mẫu hoa văn, trang trí và các tác phẩm nghệ thuật.
- Địa lý và bản đồ học:
Hình tam giác được sử dụng trong việc đo đạc và bản đồ học để xác định khoảng cách và diện tích trên bề mặt trái đất.
Các Bài Toán Minh Họa
Bài toán 1:
Cho tam giác ABC có độ dài các cạnh lần lượt là 7 cm, 8 cm và 9 cm. Tính diện tích của tam giác này.
Giải:
Áp dụng công thức Heron:
s=7+8+92=12s = \frac{7 + 8 + 9}{2} = 12s=27+8+9=12
S=12(12−7)(12−8)(12−9)S = \sqrt{12(12 – 7)(12 – 8)(12 – 9)}S=12(12−7)(12−8)(12−9) S=12×5×4×3S = \sqrt{12 \times 5 \times 4 \times 3}S=12×5×4×3 S=720≈26.83 cm2S = \sqrt{720} \approx 26.83 \, \text{cm}^2S=720≈26.83cm2
Vậy diện tích của tam giác là khoảng 26.83 cm².
Bài toán 2:
Cho tam giác vuông có hai cạnh góc vuông lần lượt là 6 cm và 8 cm. Tính diện tích của tam giác này.
Giải:
Áp dụng công thức diện tích tam giác vuông:
S=12×6×8=24 cm2S = \frac{1}{2} \times 6 \times 8 = 24 \, \text{cm}^2S=21×6×8=24cm2
Vậy diện tích của tam giác là 24 cm².
Bài viết xem thêm: Phương Thức Biểu Đạt
Kết Luận
Hình tam giác là một hình học cơ bản nhưng vô cùng quan trọng trong toán học và ứng dụng thực tế. Việc hiểu rõ các tính chất, công thức và ứng dụng của hình tam giác không chỉ giúp ích trong việc giải quyết các bài toán mà còn mở rộng hiểu biết về nhiều lĩnh vực khác nhau. Hy vọng bài viết này đã cung cấp những kiến thức cần thiết và hữu ích về hình tam giác. Chúc bạn học tốt và áp dụng hiệu quả trong cuộc sống!