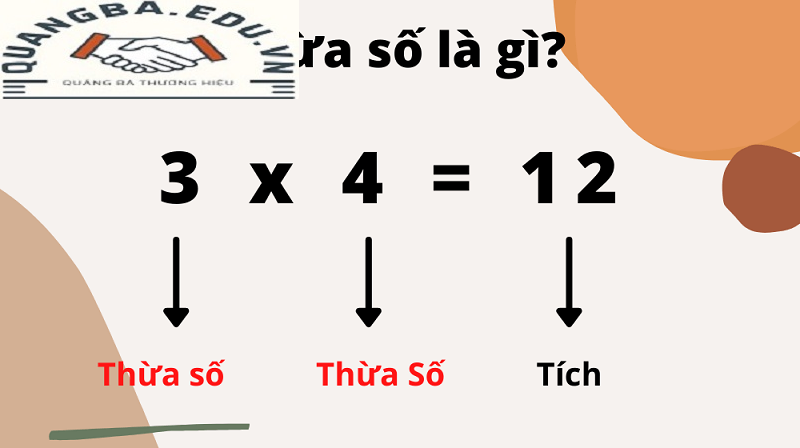
Thừa số là gì?

Thừa số là gì? – Trong toán học, thừa số là một khái niệm cơ bản và quan trọng. Thừa số là một số mà khi nhân với một số khác sẽ cho ra một sản phẩm nhất định. Hiểu rõ về thừa số không chỉ giúp chúng ta giải quyết các bài toán nhân chia một cách hiệu quả mà còn là nền tảng để tiếp cận các khái niệm toán học phức tạp hơn.
Giới thiệu về thừa số
Khi chúng ta nói về thừa số, chúng ta thường nghĩ đến các số nguyên tố và hợp số. Một số nguyên tố chỉ có hai thừa số, đó là 1 và chính nó. Trong khi đó, một số hợp số có nhiều hơn hai thừa số. Ví dụ, số 6 là một hợp số vì nó có các thừa số là 1, 2, 3 và 6. Ngược lại, số 7 là một số nguyên tố vì nó chỉ có hai thừa số là 1 và 7.
Việc xác định thừa số của một số có thể được thực hiện thông qua nhiều phương pháp khác nhau. Một trong những phương pháp phổ biến nhất là phân tích thừa số nguyên tố, nơi chúng ta chia số đó cho các số nguyên tố nhỏ nhất có thể cho đến khi không thể chia được nữa. Chẳng hạn, để tìm thừa số của 12, chúng ta có thể phân tích nó thành 2 x 2 x 3.
Bài viết liên quan: Nội Dung Sách Giáo Khoa Lớp 1
Thừa số không chỉ quan trọng trong các phép toán cơ bản mà còn đóng vai trò then chốt trong các ứng dụng toán học khác như lý thuyết số, đại số, và hình học. Chúng giúp chúng ta hiểu rõ hơn về cấu trúc của các số và cách chúng tương tác với nhau. Ngoài ra, thừa số còn có ứng dụng trong nhiều lĩnh vực thực tiễn như mật mã học, khoa học máy tính, và kỹ thuật.
Khái niệm cơ bản về thừa số
Khái niệm thừa số là một thành phần quan trọng trong toán học, đặc biệt trong lĩnh vực số học và đại số. Một thừa số của một số nguyên là một số nguyên khác có thể chia đều cho số đó mà không để lại dư. Nói cách khác, nếu bạn có một số a và một số b, b được xem là thừa số của a nếu a chia hết cho b. Ví dụ, trong phép nhân 2 x 3 = 6, cả 2 và 3 đều là thừa số của 6.
Các thừa số không chỉ giới hạn ở các số nguyên nhỏ. Một số nguyên bất kỳ có thể có nhiều thừa số khác nhau. Chẳng hạn, số 12 có các thừa số là 1, 2, 3, 4, 6, và 12. Việc tìm thừa số của một số lớn hơn có thể phức tạp hơn, đặc biệt khi số đó là một số nguyên tố, nghĩa là nó chỉ có hai thừa số là 1 và chính nó. Ví dụ, 7 chỉ có hai thừa số là 1 và 7, trong khi số 28 có các thừa số là 1, 2, 4, 7, 14, và 28.
Phân tích một số thành các thừa số cơ bản giúp đơn giản hóa các bài toán và công thức toán học. Chẳng hạn, trong đại số, việc phân tích thừa số của đa thức có thể giúp giải các phương trình phức tạp. Một cách phổ biến để phân tích số là sử dụng phương pháp phân tích thừa số nguyên tố, trong đó một số lớn được chia nhỏ thành các số nguyên tố nhỏ hơn. Ví dụ, số 60 có thể được phân tích thành các thừa số nguyên tố là 2, 2, 3, và 5 (tức là 2² x 3 x 5).
Hiểu rõ khái niệm thừa số và cách chúng hoạt động là cơ sở để tiến tới các khái niệm toán học phức tạp hơn, bao gồm tìm bội số chung nhỏ nhất, ước số chung lớn nhất, và ứng dụng trong các bài toán thực tế.
Cách tìm thừa số của một số
Để xác định thừa số của một số, phương pháp phổ biến nhất là sử dụng phép chia thử. Quá trình này bắt đầu từ số nhỏ nhất, thông thường là số 1, và kiểm tra xem số đó có thể chia hết cho số cần tìm thừa số hay không. Nếu kết quả của phép chia là không dư, nghĩa là số đó là một thừa số của số cần tìm.
Ví dụ, để tìm các thừa số của số 28, bạn bắt đầu bằng việc chia 28 cho 1. Vì bất kỳ số nào chia cho 1 cũng không dư, nên 1 là một thừa số của 28. Tiếp theo, bạn kiểm tra các số tiếp theo như 2, 3, 4, và tiếp tục như vậy. Với 28, khi bạn chia cho 2, kết quả là 14, không dư. Do đó, 2 và 14 là các thừa số của 28. Khi bạn kiểm tra với số 3, 28 không chia hết cho 3, vậy nên 3 không phải là thừa số của 28. Quá trình này tiếp tục cho đến khi bạn không thể tìm thêm thừa số nào nữa.
Để tối ưu hóa quá trình tìm thừa số, bạn cũng có thể sử dụng định lý số học cơ bản. Theo định lý này, bạn chỉ cần kiểm tra các số từ 1 đến căn bậc hai của số cần tìm thừa số. Điều này giúp giảm bớt số lượng phép chia cần thực hiện. Chẳng hạn, với số 28, bạn chỉ cần kiểm tra từ 1 đến 5 (căn bậc hai của 28 là khoảng 5.29). Điều này giúp tiết kiệm thời gian và công sức.
Việc tìm thừa số không chỉ hữu ích trong toán học mà còn ứng dụng trong nhiều lĩnh vực khác, như mã hóa, phân tích dữ liệu, và tối ưu hóa các thuật toán. Hiểu rõ cách tìm thừa số sẽ giúp bạn nắm bắt được nhiều khía cạnh quan trọng của các bài toán và vấn đề thực tiễn.
Thừa số nguyên tố
Thừa số nguyên tố là những số nguyên tố mà một số có thể được chia đều cho. Các số nguyên tố là những số tự nhiên lớn hơn 1 và chỉ có hai ước số dương là 1 và chính nó. Khi một số có thể được phân tích thành tích của các số nguyên tố, các số đó được gọi là thừa số nguyên tố của số đó.
Ví dụ, thừa số nguyên tố của số 12 là 2 và 3, vì 12 có thể được viết lại dưới dạng 2 x 2 x 3. Việc phân tích số thành các thừa số nguyên tố giúp ta hiểu rõ cấu trúc của số đó và có thể áp dụng trong nhiều lĩnh vực khác nhau của toán học và khoa học máy tính.
Thừa số nguyên tố đóng vai trò quan trọng trong phân tích số học và trong các lĩnh vực như mật mã học. Trong mật mã học, việc phân tích một số lớn thành các thừa số nguyên tố là một yếu tố cơ bản để xác định tính an toàn của các hệ thống mã hóa. Các thuật toán mã hóa như RSA dựa vào việc khó khăn trong việc phân tích một số rất lớn thành các thừa số nguyên tố, điều này giúp bảo mật thông tin.
Quá trình tìm thừa số nguyên tố của một số không phải lúc nào cũng đơn giản, đặc biệt là với các số rất lớn. Tuy nhiên, với các công cụ và thuật toán hiện đại, việc này đã trở nên dễ dàng và hiệu quả hơn rất nhiều. Các thuật toán như phương pháp sàng Eratosthenes, phương pháp phân tích thử nghiệm và phương pháp phân tích bằng cây đều được sử dụng rộng rãi để tìm thừa số nguyên tố.
Hiểu biết về thừa số nguyên tố không chỉ giúp ta trong việc giải quyết các bài toán toán học mà còn cung cấp nền tảng cho nhiều ứng dụng trong khoa học và công nghệ.
Ứng dụng của thừa số trong toán học
Thừa số là các số hoặc biểu thức nhân với nhau để tạo thành một số hoặc biểu thức khác. Trong toán học, thừa số có vai trò quan trọng và được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Một trong những ứng dụng phổ biến nhất của thừa số là trong việc đơn giản hóa các phép tính phức tạp. Bằng cách phân tích một số thành các thừa số nguyên tố, chúng ta có thể thực hiện các phép tính như nhân, chia dễ dàng hơn.
Thừa số cũng rất hữu ích trong việc tìm ra ước chung lớn nhất (GCD) của hai hoặc nhiều số. GCD là số nguyên lớn nhất chia hết cho tất cả các số trong tập hợp đó. Việc tìm GCD giúp giải quyết nhiều bài toán trong số học và đại số, chẳng hạn như rút gọn phân số hoặc giải các phương trình đồng dư.
Trong lý thuyết số, thừa số đóng một vai trò quan trọng. Việc phân tích số thành các thừa số nguyên tố là cơ sở cho nhiều định lý và chứng minh trong lý thuyết số, chẳng hạn như Định lý Cơ bản của Số học. Ngoài ra, thừa số còn được ứng dụng trong các dạng mã hóa dữ liệu, một lĩnh vực quan trọng của mật mã học. Các thuật toán mã hóa dựa trên việc phân tích số học và thừa số để đảm bảo tính bảo mật của thông tin.
Như vậy, thừa số không chỉ giúp đơn giản hóa các phép tính mà còn có nhiều ứng dụng khác nhau trong toán học, từ số học cơ bản đến lý thuyết số và mã hóa dữ liệu. Việc hiểu và sử dụng thừa số một cách hiệu quả sẽ giúp chúng ta giải quyết các bài toán toán học một cách dễ dàng và chính xác hơn.
Thừa số và phân tích đa thức
Trong lĩnh vực đại số, thừa số hóa đa thức đóng vai trò quan trọng trong việc giải phương trình và phân tích cấu trúc của đa thức. Quá trình này liên quan đến việc phân tích một đa thức thành các thừa số là các đa thức bậc thấp hơn. Khi một đa thức được thừa số hóa thành công, ta có thể sử dụng các thừa số này để giải phương trình liên quan một cách dễ dàng hơn.
Một trong những kỹ thuật cơ bản để thừa số hóa đa thức là tìm nghiệm của đa thức đó. Khi đã xác định được một nghiệm, ta có thể sử dụng nó để chia đa thức ban đầu thành hai phần, trong đó một phần là nhân tử chứa nghiệm đó, và phần còn lại là đa thức bậc thấp hơn. Quá trình này có thể được lặp lại cho đến khi đa thức được phân tích hoàn toàn thành các thừa số nguyên.
Thừa số hóa đa thức không chỉ giúp giải phương trình mà còn cung cấp cái nhìn sâu sắc về cấu trúc và tính chất của đa thức. Chẳng hạn, bằng cách thừa số hóa, ta có thể xác định được các điểm mà đa thức cắt trục hoành, các điểm cực trị, và các khoảng tăng giảm của hàm số tương ứng. Điều này đặc biệt hữu ích trong việc nghiên cứu hàm số và ứng dụng trong các bài toán thực tế.
Việc thừa số hóa cũng đóng vai trò quan trọng trong lý thuyết số và các lĩnh vực khác của toán học. Chẳng hạn, trong lý thuyết số, việc tìm các thừa số nguyên của một số nguyên lớn là một vấn đề cơ bản và có nhiều ứng dụng trong mã hóa và bảo mật thông tin. Tương tự, trong đại số tuyến tính, việc thừa số hóa ma trận là một kỹ thuật quan trọng để giải hệ phương trình tuyến tính và phân tích các đặc trưng của ma trận.
Thừa số và số học phổ thông
Trong số học phổ thông, việc tìm thừa số của một số là một kỹ năng căn bản và quan trọng. Học sinh thường bắt đầu với việc phân tích số thành các thừa số nguyên tố, một quá trình giúp họ hiểu rõ hơn về cấu trúc của các số nguyên. Phân tích thừa số nguyên tố là quá trình phân tách một số thành các thừa số mà không thể phân chia thêm được nữa, ngoại trừ 1 và chính số đó.
Quá trình này không chỉ giúp học sinh nắm vững các khái niệm cơ bản của số học, mà còn là nền tảng để giải quyết các bài toán phức tạp hơn như tìm ước chung lớn nhất (ƯCLN) và bội số chung nhỏ nhất (BCNN). Chẳng hạn, để tìm ƯCLN của hai số, học sinh cần phân tích từng số thành các thừa số nguyên tố, sau đó xác định các thừa số chung và nhân chúng lại với nhau. Tương tự, để tìm BCNN, học sinh sẽ lấy tất cả các thừa số nguyên tố xuất hiện trong cả hai số, với số lần xuất hiện nhiều nhất, và nhân chúng lại.
Bài viết xem thêm: Danh Từ Chung và Danh Từ Riêng
Những kỹ năng này không chỉ được áp dụng trong chương trình toán học tiểu học mà còn là cơ sở cho các khái niệm toán học phức tạp hơn ở cấp trung học. Việc nắm vững phân tích thừa số và các ứng dụng của nó giúp học sinh phát triển tư duy logic và kỹ năng giải quyết vấn đề. Hơn nữa, hiểu biết về thừa số còn có thể giúp ích trong các lĩnh vực khác như khoa học máy tính, mật mã học và lý thuyết số.
Do đó, việc học và thực hành tìm thừa số được coi là một phần không thể thiếu trong chương trình giáo dục toán học, giúp học sinh xây dựng nền tảng vững chắc cho các khái niệm nâng cao hơn trong tương lai.