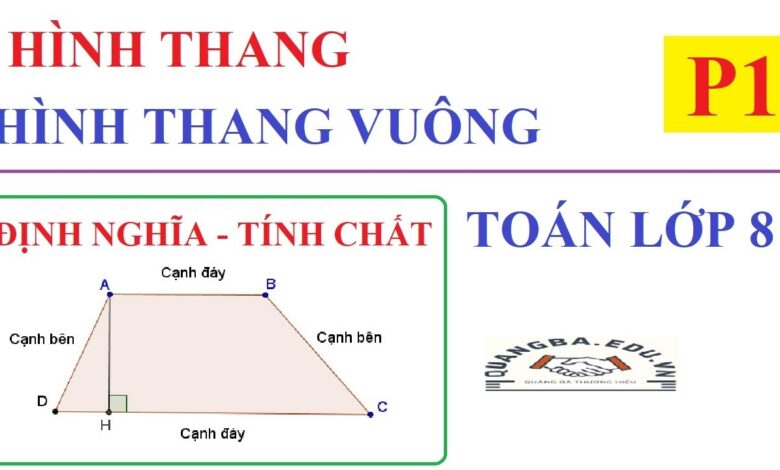
Tính Chất Hình Thang Vuông
Tính Chất Hình Thang Vuông – Hình thang vuông là một hình học đặc biệt trong toán học cơ bản, có nhiều ứng dụng thực tế và lý thuyết. Đặc điểm nổi bật nhất của hình thang vuông là sự hiện diện của một góc vuông giữa hai cạnh kề nhau, tạo nên một hình dạng dễ nhận biết và dễ vẽ. Điều này khác biệt so với các loại hình thang khác, nơi không có yêu cầu cụ thể về góc vuông.
Giới thiệu về hình thang vuông
Trong hình thang vuông, hai cạnh đáy song song với nhau, trong khi hai cạnh bên không song song. Cạnh bên vuông góc với hai cạnh đáy, tạo thành góc 90 độ. Sự đơn giản và tính dễ hiểu của hình thang vuông khiến nó trở thành một trong những bài học đầu tiên mà học sinh tiểu học tiếp cận khi học về hình học.
Hình thang vuông không chỉ quan trọng trong giáo dục mà còn có nhiều ứng dụng trong cuộc sống hàng ngày. Các kỹ sư, kiến trúc sư, và nhà thiết kế thường sử dụng các nguyên tắc của hình thang vuông trong công việc của họ. Chẳng hạn, trong xây dựng, hình thang vuông có thể được sử dụng để thiết kế các cấu trúc mái nhà, cầu thang, và nhiều phần khác của công trình.
Hơn nữa, việc hiểu rõ về tính chất của hình thang vuông giúp học sinh phát triển khả năng tư duy logic và kỹ năng giải quyết vấn đề. Những bài tập liên quan đến hình thang vuông thường yêu cầu học sinh xác định độ dài các cạnh, diện tích, hoặc chu vi của hình, từ đó củng cố kiến thức về các công thức toán học cơ bản.
Trong bài viết này, chúng ta sẽ cùng khám phá chi tiết hơn về các tính chất đặc trưng của hình thang vuông, cũng như những ví dụ cụ thể về cách áp dụng nó trong cuộc sống và học tập.
Định nghĩa và đặc điểm của hình thang vuông
Hình thang vuông là một loại hình thang đặc biệt với đặc điểm nổi bật là có một góc vuông, tức là một góc 90 độ. Điều này có nghĩa rằng một trong hai cặp cạnh kề của hình thang vuông tạo thành một góc vuông. Hình thang vuông không chỉ là một khái niệm trừu tượng trong hình học mà còn có ứng dụng trong nhiều lĩnh vực thực tiễn như thiết kế kiến trúc và kỹ thuật xây dựng.
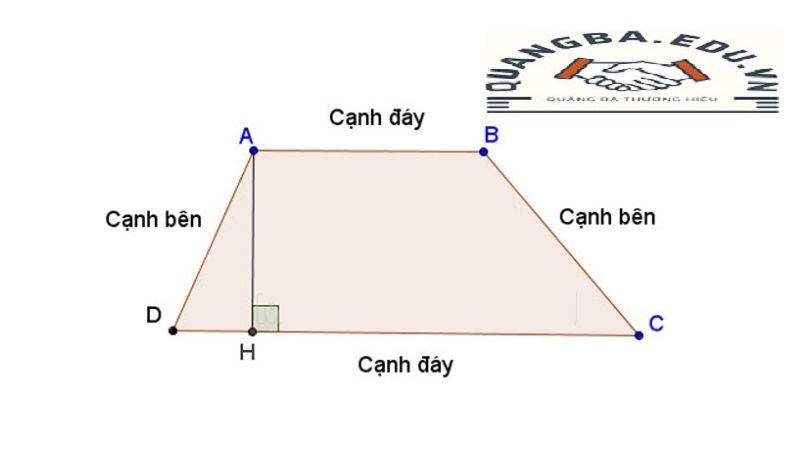
Trong cấu trúc của hình thang vuông, hai cạnh song song của nó được gọi là đáy lớn và đáy nhỏ. Đáy lớn là cạnh có chiều dài lớn hơn, trong khi đáy nhỏ là cạnh có chiều dài ngắn hơn. Điều này giúp dễ dàng phân biệt và định dạng hình thang vuông trong thực tế. Điểm đặc biệt nữa của hình thang vuông là cạnh vuông góc với cả hai đáy, là chiều cao của hình thang vuông. Chiều cao này đóng vai trò quan trọng trong việc tính toán diện tích và chu vi của hình thang vuông.
Hình thang vuông không chỉ có ứng dụng trong học tập mà còn trong nhiều lĩnh vực khác. Ví dụ, trong thiết kế kiến trúc, hình thang vuông có thể được sử dụng để tạo ra các góc vuông chính xác, giúp công trình đạt độ chính xác cao hơn. Trong kỹ thuật xây dựng, hình thang vuông thường được sử dụng để thiết kế các chi tiết cấu trúc, đảm bảo tính ổn định và an toàn cho công trình.
Bài viết liên quan: Hiệu là phép tính gì?
Như vậy, hình thang vuông không chỉ là một khái niệm hình học cơ bản mà còn có nhiều ứng dụng thực tiễn, đóng góp vào nhiều lĩnh vực khác nhau trong cuộc sống. Việc hiểu rõ định nghĩa và đặc điểm của hình thang vuông sẽ giúp chúng ta áp dụng nó một cách hiệu quả trong các bài toán và công việc thực tiễn.
Tính chất của hình thang vuông
Hình thang vuông là một dạng đặc biệt của hình thang với nhiều tính chất đặc trưng riêng biệt. Một trong những tính chất nổi bật nhất của hình thang vuông là sự tồn tại của một góc vuông. Góc vuông này tạo nên một đặc điểm hình học đặc biệt, giúp dễ dàng nhận diện và tính toán các yếu tố liên quan.
Hình thang vuông có hai cạnh song song, gọi là đáy lớn và đáy nhỏ. Đáy lớn là cạnh dài hơn trong hai cạnh song song, trong khi đáy nhỏ là cạnh ngắn hơn. Sự song song của hai cạnh này đóng vai trò quan trọng trong việc xác định hình dạng và đặc điểm của hình thang vuông.
Một tính chất quan trọng khác của hình thang vuông là chiều cao vuông góc với hai đáy. Chiều cao này là khoảng cách ngắn nhất giữa hai cạnh song song, và nó đóng vai trò quan trọng trong việc tính toán diện tích của hình thang vuông.
Trong mọi hình thang vuông, tổng số góc luôn luôn bằng 360 độ. Điều này là một đặc điểm chung của tất cả các hình tứ giác và giúp đảm bảo tính nhất quán trong các phép tính liên quan đến góc.
Những tính chất này của hình thang vuông giúp cho việc tính toán diện tích và chu vi trở nên dễ dàng hơn. Việc biết trước rằng một góc trong hình thang vuông là góc vuông, và các cạnh đáy là song song, cho phép áp dụng các công thức toán học một cách trực tiếp và hiệu quả. Diện tích của hình thang vuông có thể được tính bằng cách sử dụng công thức diện tích của hình thang thông thường, với chiều cao và chiều dài hai đáy đã biết.
Cách tính diện tích hình thang vuông
Để tính diện tích hình thang vuông, người học cần nắm vững công thức cơ bản: Diện tích = (Đáy lớn + Đáy nhỏ) * Chiều cao / 2. Công thức này không chỉ quan trọng trong việc giải các bài toán học thuật mà còn hữu ích trong các ứng dụng thực tế. Hình thang vuông là một dạng hình học đặc biệt, với hai cạnh đối song song và một cạnh vuông góc với hai đáy.
Ví dụ, để tính diện tích của một hình thang vuông với đáy lớn là 8 cm, đáy nhỏ là 5 cm, và chiều cao là 6 cm, ta áp dụng công thức như sau:
Diện tích = (8 cm + 5 cm) * 6 cm / 2 = 13 cm * 6 cm / 2 = 39 cm².
Công thức này giúp người học dễ dàng xác định diện tích của bất kỳ hình thang vuông nào, chỉ cần biết các thông số cần thiết là chiều dài của hai đáy và chiều cao. Điều này rất hữu ích trong việc giải quyết các bài toán về hình học trong sách giáo khoa, bài kiểm tra, và thi cử.
Hơn nữa, việc hiểu rõ và áp dụng đúng công thức này cũng giúp người học phát triển khả năng tư duy logic và kỹ năng giải quyết vấn đề, những yếu tố quan trọng không chỉ trong học tập mà còn trong cuộc sống hàng ngày. Ví dụ, trong xây dựng hoặc thiết kế, việc tính toán chính xác diện tích các hình thang vuông có thể giúp tối ưu hóa không gian và vật liệu.
Ngoài ra, công thức này cũng có thể được sử dụng để giải quyết các bài toán nâng cao hơn, chẳng hạn như tính diện tích các hình phức tạp hơn bằng cách chia chúng thành các hình thang vuông nhỏ hơn. Đây là một kỹ năng quan trọng giúp người học tiến xa hơn trong lĩnh vực toán học và các ngành khoa học liên quan.
Cách tính chu vi hình thang vuông
Chu vi của hình thang vuông là tổng độ dài của tất cả các cạnh của nó. Để tính chu vi một cách chính xác, ta cần biết độ dài của đáy lớn, đáy nhỏ, và hai cạnh bên. Công thức tính chu vi hình thang vuông như sau:
Chu vi = Đáy lớn + Đáy nhỏ + Hai cạnh bên
Việc hiểu rõ công thức này là rất quan trọng vì nó giúp học sinh nắm vững kiến thức cơ bản về hình học và có thể áp dụng vào các bài toán thực tế. Khi biết được chiều dài của từng cạnh, học sinh có thể dễ dàng tính toán chu vi bằng cách cộng tổng các giá trị lại với nhau.
Hãy xem xét một ví dụ cụ thể để làm rõ hơn về cách tính chu vi hình thang vuông. Giả sử chúng ta có một hình thang vuông với các độ dài sau: đáy lớn là 10 cm, đáy nhỏ là 6 cm, và hai cạnh bên lần lượt là 5 cm và 7 cm. Áp dụng công thức tính chu vi, ta có:
Chu vi = 10 cm + 6 cm + 5 cm + 7 cm = 28 cm
Như vậy, chu vi của hình thang vuông trong ví dụ này là 28 cm. Bằng cách thực hiện các bước đơn giản như trên, học sinh có thể tự tin tính toán chu vi của bất kỳ hình thang vuông nào. Đây là một kỹ năng cơ bản nhưng rất cần thiết trong việc giải quyết các bài toán liên quan đến hình học và thực tế.
Thực hành thường xuyên và làm quen với các dạng bài tập khác nhau sẽ giúp học sinh củng cố và nâng cao khả năng tính toán, từ đó áp dụng hiệu quả trong các tình huống thực tiễn hàng ngày.
Ứng dụng của hình thang vuông trong thực tế
Hình thang vuông là một hình học quan trọng, có nhiều ứng dụng trong cuộc sống hàng ngày, đặc biệt trong các lĩnh vực như kiến trúc và xây dựng. Với đặc tính đặc biệt của mình, hình thang vuông thường được sử dụng trong thiết kế cầu thang, mái nhà và nhiều công trình xây dựng khác.
Trong ngành kiến trúc, hình thang vuông giúp tạo ra các thiết kế độc đáo và hiệu quả. Ví dụ, cầu thang hình thang vuông không chỉ tiết kiệm không gian mà còn đảm bảo an toàn khi sử dụng. Điều này đặc biệt quan trọng trong các tòa nhà cao tầng hoặc các không gian hạn chế.
Trong xây dựng, hình thang vuông được áp dụng để tạo ra các kết cấu chịu lực tốt hơn. Mái nhà dạng hình thang vuông không chỉ giúp thoát nước mưa hiệu quả mà còn tạo ra vẻ đẹp thẩm mỹ cho ngôi nhà. Bên cạnh đó, việc sử dụng hình thang vuông trong kết cấu dầm cầu cũng giúp tăng khả năng chịu lực và độ bền của công trình.
Không chỉ dừng lại ở kiến trúc và xây dựng, hình thang vuông còn được ứng dụng trong nhiều lĩnh vực kỹ thuật khác. Ví dụ, trong thiết kế các bộ phận cơ khí, hình thang vuông giúp tối ưu hóa không gian và tăng độ bền của sản phẩm. Hơn nữa, trong ngành công nghiệp chế tạo, hình thang vuông được sử dụng để thiết kế các khuôn mẫu chính xác, giúp quá trình sản xuất trở nên hiệu quả hơn.
Hiểu rõ về hình thang vuông và các tính chất của nó giúp chúng ta áp dụng vào thực tế một cách hiệu quả hơn. Nhờ đó, chúng ta có thể tạo ra những công trình và sản phẩm tối ưu, đáp ứng được các yêu cầu kỹ thuật và thẩm mỹ. Việc nắm vững các ứng dụng của hình thang vuông là nền tảng quan trọng để phát triển các giải pháp sáng tạo và hiệu quả trong nhiều lĩnh vực khác nhau.
Bài tập áp dụng về hình thang vuông
Để nắm vững kiến thức về hình thang vuông, học sinh cần thực hành qua các bài tập. Dưới đây là một số bài tập cơ bản và nâng cao giúp học sinh củng cố kiến thức về hình học, đặc biệt là về hình thang vuông.
Bài tập cơ bản:
- Cho hình thang vuông ABCD với góc A và D là góc vuông. Biết AB = 5 cm, AD = 4 cm và CD = 7 cm. Hãy tính diện tích của hình thang vuông này.
- Cho hình thang vuông EFGH với góc E và H là góc vuông. Biết EF = 6 cm, EH = 3 cm và GH = 9 cm. Hãy tính chu vi của hình thang vuông này.
Bài tập nâng cao:
- Cho hình thang vuông KLMN với góc K và N là góc vuông. Biết rằng đáy lớn KL dài gấp đôi đáy nhỏ MN, và chiều cao KN = 8 cm. Nếu diện tích của hình thang vuông là 96 cm², hãy tính độ dài của các cạnh KL và MN.
- Cho hình thang vuông PQRS với góc P và S là góc vuông. Biết PQ = 12 cm, PS = 5 cm và diện tích của hình thang vuông là 60 cm². Tính độ dài của cạnh RS.
Thông qua các bài tập này, học sinh có thể rèn luyện kỹ năng tính toán diện tích, chu vi và giải quyết các bài toán liên quan đến hình thang vuông. Việc thực hành thường xuyên sẽ giúp học sinh nắm vững kiến thức và áp dụng hiệu quả trong các bài kiểm tra và kỳ thi.
Kết luận nội dung
Hình thang vuông là một khái niệm quan trọng trong toán học cơ bản, mang lại nhiều ứng dụng thực tế trong cuộc sống hàng ngày. Việc hiểu rõ về các tính chất đặc trưng, phương pháp tính diện tích và chu vi của hình thang vuông không chỉ giúp học sinh nắm bắt kiến thức một cách vững vàng mà còn góp phần nâng cao kỹ năng giải quyết vấn đề.
Hình thang vuông có các cạnh song song và một góc vuông, tính chất này giúp dễ dàng áp dụng các công thức toán học để tính toán chính xác. Khả năng ứng dụng của hình thang vuông không chỉ giới hạn trong lĩnh vực giáo dục mà còn mở rộng ra nhiều ngành khác như kiến trúc, kỹ thuật và thiết kế. Sự hiểu biết về hình thang vuông giúp chúng ta có thể tính toán diện tích mặt bằng, thiết kế các công trình xây dựng hay phân tích các hình dạng trong tự nhiên một cách hiệu quả.
Bài viết xem thêm: Thương là phép tính gì?
Thông qua việc học và thực hành với hình thang vuông, học sinh không chỉ nắm vững kiến thức cơ bản mà còn phát triển tư duy logic và khả năng áp dụng kiến thức vào thực tiễn. Điều này đặc biệt quan trọng trong việc giúp các em chuẩn bị cho các kỳ thi quan trọng, cũng như xây dựng nền tảng vững chắc cho các cấp học cao hơn.
Tóm lại, nắm vững tính chất, cách tính diện tích và chu vi của hình thang vuông là một bước quan trọng trong việc phát triển kiến thức toán học cơ bản. Việc này không chỉ giúp học sinh học tốt hơn mà còn mang lại nhiều lợi ích trong cuộc sống hàng ngày và công việc chuyên môn. Qua đó, hình thang vuông chứng tỏ vai trò quan trọng và không thể thiếu trong chương trình học toán học hiện đại.