Tính Chu Vi Hình Thoi
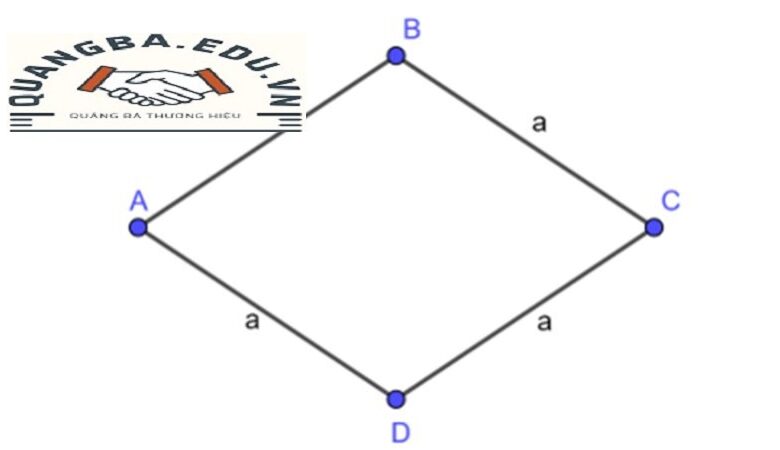
Tính Chu Vi Hình Thoi – Hình thoi là một loại tứ giác đặc biệt trong hình học, nổi bật với bốn cạnh bằng nhau và các cặp góc đối bằng nhau. Đặc điểm này không chỉ làm cho hình thoi trở nên đặc biệt trong các bài toán hình học mà còn khiến nó có nhiều ứng dụng thực tiễn trong đời sống hàng ngày.
Giới Thiệu về Hình Thoi
Một trong những đặc điểm quan trọng của hình thoi là các đường chéo của nó cắt nhau tại một điểm và chia đôi nhau, tạo thành bốn tam giác vuông. Các đường chéo này cũng vuông góc với nhau, điều này giúp đơn giản hóa nhiều phép tính liên quan đến hình thoi. Hình thoi là một trường hợp đặc biệt của hình bình hành, vì vậy, nó cũng kế thừa tất cả các tính chất của hình bình hành như hai cặp cạnh đối song song và bằng nhau.
Trong đời sống, hình thoi thường xuyên xuất hiện trong các thiết kế kiến trúc, trang trí, và cả trong các lĩnh vực khoa học kỹ thuật. Ví dụ, trong kiến trúc, hình thoi thường được sử dụng làm mô hình trang trí trên các bề mặt tường hay sàn nhà, tạo ra những hoa văn đẹp mắt và thu hút sự chú ý. Trong lĩnh vực trang sức, hình thoi thường được dùng để cắt kim cương, tạo nên những viên đá quý lấp lánh và sang trọng.
Bài viết liên quan: Số Bị Chia Là Gì?
Với những ứng dụng phong phú và những tính chất đặc biệt, việc nắm vững các công thức và phương pháp tính toán liên quan đến hình thoi là vô cùng quan trọng. Điều này không chỉ giúp giải quyết các bài toán hình học một cách hiệu quả mà còn mở rộng khả năng ứng dụng trong nhiều lĩnh vực khác nhau. Bài viết này sẽ tiếp tục giới thiệu chi tiết về cách tính chu vi hình thoi và những ứng dụng thực tiễn của nó.
Định Nghĩa Chu Vi Hình Thoi
Chu vi hình thoi được định nghĩa là tổng độ dài của tất cả các cạnh của hình thoi. Hình thoi là một tứ giác có bốn cạnh bằng nhau và các góc đối diện bằng nhau. Do đó, để tính chu vi của một hình thoi, ta chỉ cần biết độ dài của một cạnh duy nhất và nhân nó với bốn. Công thức này trở nên rất đơn giản và dễ nhớ, giúp chúng ta nhanh chóng xác định chu vi của hình thoi một cách chính xác.
Công thức tính chu vi hình thoi được viết như sau:
Chu vi = 4 x độ dài cạnh
Ví dụ, nếu một hình thoi có độ dài cạnh là 5 cm, thì chu vi của nó sẽ là:
Chu vi = 4 x 5 cm = 20 cm
Việc hiểu rõ cách tính chu vi hình thoi không chỉ quan trọng trong các bài toán hình học mà còn có nhiều ứng dụng thực tiễn. Trong kiến trúc và xây dựng, việc xác định chính xác chu vi của các hình thoi có thể giúp tính toán lượng vật liệu cần thiết, đảm bảo độ chính xác của các công trình. Trong thiết kế đồ họa hoặc trang trí nội thất, việc sử dụng hình thoi và tính toán chu vi của chúng có thể tạo ra các mẫu thiết kế đẹp mắt và cân đối.
Như vậy, chu vi hình thoi không chỉ là một khái niệm lý thuyết mà còn có giá trị ứng dụng cao trong thực tế. Hiểu và áp dụng đúng công thức tính chu vi hình thoi sẽ giúp chúng ta giải quyết nhiều vấn đề trong các lĩnh vực khác nhau một cách hiệu quả và nhanh chóng.
Công Thức Tính Chu Vi Hình Thoi
Chu vi của một hình thoi có thể được tính toán dễ dàng bằng công thức P = 4a, trong đó ‘P’ là chu vi và ‘a’ là độ dài của một cạnh hình thoi. Công thức này xuất phát từ đặc tính đặc biệt của hình thoi: tất cả các cạnh của nó đều có độ dài bằng nhau. Do đó, để tìm chu vi của hình thoi, chúng ta chỉ cần biết độ dài của một cạnh và nhân nó với 4.
Để hiểu rõ hơn về công thức này, hãy xem qua một ví dụ cụ thể. Giả sử chúng ta có một hình thoi với độ dài mỗi cạnh là 5 cm. Áp dụng công thức P = 4a, chúng ta có:
P = 4a = 4 × 5 = 20 cm
Vậy, chu vi của hình thoi này là 20 cm. Đây là một cách tính toán cực kỳ đơn giản và nhanh chóng, giúp tiết kiệm thời gian và công sức, đặc biệt trong các bài toán hình học cơ bản hoặc ứng dụng thực tiễn.
Việc nắm vững công thức tính chu vi hình thoi không chỉ hữu ích trong các bài toán học mà còn có thể áp dụng trong nhiều lĩnh vực khác nhau của cuộc sống. Ví dụ, khi bạn cần tính toán chi phí làm hàng rào xung quanh một mảnh đất hình thoi, việc biết chu vi sẽ giúp bạn ước lượng được số vật liệu cần thiết một cách chính xác.
Trong xây dựng và kiến trúc, công thức này cũng rất hữu ích khi cần tính toán kích thước và chi phí cho các công trình có hình dáng tương tự. Như vậy, hiểu rõ và áp dụng đúng công thức tính chu vi hình thoi sẽ giúp bạn giải quyết nhiều vấn đề thực tiễn một cách hiệu quả.
Ví Dụ Cụ Thể về Tính Chu Vi Hình Thoi
Để hiểu rõ hơn về cách tính chu vi hình thoi, chúng ta sẽ cùng xem xét một số ví dụ cụ thể. Những ví dụ này sẽ được giải chi tiết từng bước nhằm giúp người đọc dễ dàng theo dõi và áp dụng vào các bài toán tương tự.
Ví dụ 1: Giả sử chúng ta có một hình thoi với cạnh dài 5 cm. Để tính chu vi của hình thoi này, chúng ta sẽ sử dụng công thức:
Chu vi hình thoi = 4 x cạnh
Áp dụng công thức trên, ta có:
Chu vi = 4 x 5 cm = 20 cm
Vậy chu vi của hình thoi này là 20 cm.
Ví dụ 2: Xét một hình thoi khác có cạnh dài 7 cm. Tương tự như ví dụ trước, chúng ta sẽ sử dụng công thức chu vi để tính toán:
Chu vi = 4 x 7 cm = 28 cm
Do đó, chu vi của hình thoi này là 28 cm.
Ví dụ 3: Giả sử một hình thoi có cạnh dài 12 cm. Để tìm chu vi, chúng ta tiếp tục áp dụng công thức:
Chu vi = 4 x 12 cm = 48 cm
Như vậy, chu vi của hình thoi này là 48 cm.
Những ví dụ trên minh họa rõ ràng cách tính chu vi hình thoi khi biết độ dài của một cạnh. Bằng việc áp dụng công thức đơn giản này, chúng ta có thể nhanh chóng và chính xác tính được chu vi của bất kỳ hình thoi nào chỉ với thông tin về độ dài của một cạnh.
Ứng Dụng Thực Tiễn của Chu Vi Hình Thoi
Chu vi hình thoi không chỉ là một khái niệm toán học mà còn có nhiều ứng dụng thực tiễn trong cuộc sống. Một trong những lĩnh vực áp dụng phổ biến nhất là kiến trúc. Trong quá trình thiết kế và xây dựng các công trình, việc tính toán chu vi hình thoi giúp các kiến trúc sư xác định chính xác kích thước và hình dạng của các chi tiết kiến trúc. Điều này đặc biệt quan trọng khi thiết kế các yếu tố trang trí hoặc các kết cấu phức tạp, đảm bảo tính thẩm mỹ và hiệu quả sử dụng không gian.
Trong kỹ thuật, chu vi hình thoi cũng được sử dụng để tính toán và thiết kế các bộ phận máy móc. Ví dụ, trong ngành cơ khí, nhiều bộ phận của máy móc có hình dạng hình thoi, và việc tính toán chu vi giúp kỹ sư xác định chính xác các thông số kỹ thuật, từ đó đảm bảo độ bền và hiệu suất của sản phẩm. Ngoài ra, chu vi hình thoi còn giúp trong việc lập kế hoạch bảo trì và sửa chữa, nhờ đó giảm thiểu thời gian ngừng hoạt động và chi phí phát sinh.
Không chỉ trong kiến trúc và kỹ thuật, chu vi hình thoi còn có vai trò quan trọng trong lĩnh vực thiết kế. Các nhà thiết kế thời trang và đồ họa thường sử dụng hình thoi để tạo ra các mẫu mã độc đáo và hấp dẫn. Việc tính toán chu vi hình thoi giúp họ kiểm soát tốt hơn các yếu tố hình học và tỷ lệ, từ đó tạo ra các sản phẩm có tính thẩm mỹ cao và hài hòa về mặt thị giác. Trong thiết kế nội thất, hình thoi cũng được ứng dụng để tạo ra các họa tiết trang trí trên tường, sàn nhà, và các vật dụng nội thất, mang lại không gian sống động và sáng tạo.
Bài Tập Thực Hành
Để củng cố kiến thức về cách tính chu vi hình thoi, dưới đây là một số bài tập thực hành với độ khó khác nhau. Mỗi bài tập đều đi kèm với lời giải chi tiết để người đọc có thể kiểm tra và so sánh kết quả của mình.
Bài Tập 1:
Một hình thoi có độ dài của một cạnh là 5 cm. Hãy tính chu vi của hình thoi này.
Lời giải:
Chu vi của hình thoi được tính bằng công thức: P = 4a, trong đó a là độ dài của một cạnh.
Áp dụng công thức, ta có: P = 4 x 5 = 20 cm.
Bài Tập 2:
Một hình thoi có tổng độ dài của hai đường chéo là 24 cm và độ dài của một trong hai đường chéo là 10 cm. Hãy tính độ dài của cạnh hình thoi và sau đó tính chu vi của nó.
Lời giải:
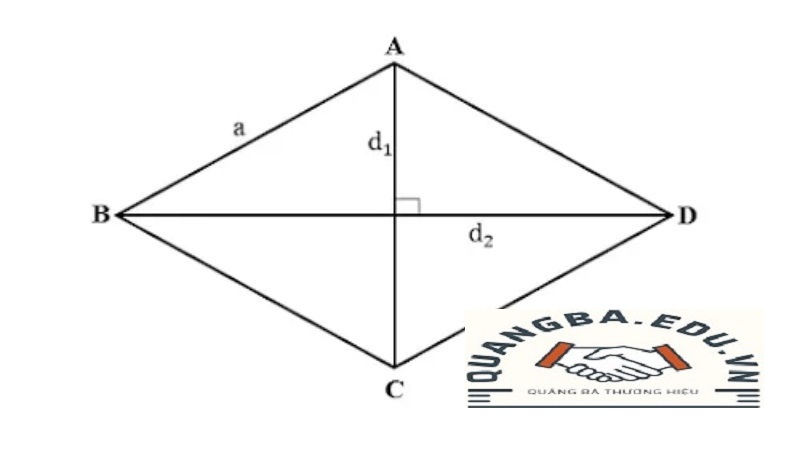
Ta gọi độ dài của hai đường chéo là d1 và d2, với d1 = 10 cm và d1 + d2 = 24 cm. Khi đó, d2 = 24 – 10 = 14 cm.
Độ dài cạnh hình thoi được tính bằng công thức: a = √((d1/2)² + (d2/2)²).
Áp dụng công thức, ta có: a = √((10/2)² + (14/2)²) = √(5² + 7²) = √(25 + 49) = √74 ≈ 8.6 cm.
Chu vi của hình thoi là: P = 4a = 4 x 8.6 ≈ 34.4 cm.
Bài Tập 3:
Một hình thoi có chu vi là 36 cm. Hãy tính độ dài của một cạnh và sau đó tính tổng độ dài của hai đường chéo.
Lời giải:
Chu vi của hình thoi được tính bằng công thức: P = 4a. Từ đó, ta có: a = P/4 = 36/4 = 9 cm.
Tổng độ dài của hai đường chéo được tính bằng công thức: d1² + d2² = 4a².
Áp dụng công thức, ta có: d1² + d2² = 4 x 9² = 4 x 81 = 324.
Do đó, tổng độ dài của hai đường chéo là: √324 = 18 cm.
Hy vọng rằng các bài tập trên sẽ giúp quý độc giả nắm vững hơn về cách tính chu vi hình thoi và ứng dụng vào các bài toán thực tiễn.
Lỗi Thường Gặp Khi Tính Chu Vi Hình Thoi
Trong quá trình tính chu vi hình thoi, có một số lỗi thường gặp mà người học cần lưu ý để tránh sai sót. Điều này không chỉ giúp đảm bảo tính chính xác mà còn tăng cường hiệu quả học tập và ứng dụng thực tế.
Một trong những lỗi phổ biến nhất là nhầm lẫn giữa các khái niệm cơ bản. Nhiều người thường nhầm lẫn giữa đường chéo và cạnh của hình thoi. Đường chéo là đoạn thẳng nối hai đỉnh đối diện của hình thoi, trong khi cạnh là đoạn thẳng nối hai đỉnh kề nhau. Để tính chu vi, cần sử dụng độ dài của cạnh, không phải độ dài của đường chéo. Việc nhầm lẫn này có thể dẫn đến sai lệch lớn trong kết quả.
Một lỗi khác là không kiểm tra tính chính xác của các số liệu đầu vào. Trong nhiều trường hợp, người học sử dụng các số liệu không đúng hoặc không phù hợp, dẫn đến kết quả sai. Việc kiểm tra lại các số liệu trước khi tính toán là rất quan trọng để đảm bảo tính chính xác.
Thêm vào đó, một số người học còn gặp khó khăn trong việc áp dụng đúng công thức. Công thức tính chu vi hình thoi rất đơn giản, nhưng nếu không nắm vững, người học có thể áp dụng sai hoặc quên một số bước quan trọng. Do đó, việc ôn tập và hiểu rõ công thức là rất cần thiết.
Cuối cùng, việc thiếu kiên nhẫn và không tập trung cũng là nguyên nhân dẫn đến các lỗi khi tính chu vi hình thoi. Tính toán đòi hỏi sự chính xác và tập trung cao độ, bởi chỉ một sai lầm nhỏ cũng có thể làm thay đổi kết quả hoàn toàn.
Bài viết xem thêm: Định Luật Phản Xạ Ánh Sáng
Kết Luận nội dung
Trong phạm vi bài viết này, chúng ta đã đi sâu tìm hiểu về cách tính chu vi hình thoi, bao gồm công thức cơ bản và những ứng dụng thực tiễn. Chu vi hình thoi là tổng độ dài của bốn cạnh của nó, và công thức tính chu vi đơn giản là nhân độ dài một cạnh với bốn. Việc hiểu và áp dụng chính xác công thức này không chỉ giúp trong việc giải quyết các bài toán hình học mà còn có nhiều ứng dụng trong thực tế, như trong thiết kế kiến trúc, kỹ thuật, và các lĩnh vực liên quan đến đo đạc và xây dựng.